Question

A vector A points vertically upward and B points towards north. The vector product \[\overrightarrow A \times \overrightarrow B\] is:
$(A)$ Null vector
$(B)$ Along west
$(C)$ Along east
$(D)$ Vertically downward

Answer 1

Hint: Draw a clear picture of the direction of the vectors along three axes. Note that, vertically upward means the direction along the normal to the plane of the paper in which we are drawing.
After getting the axis of the vectors represent the vectors with unit vectors related to those axes.
Here in the problem cross product is needed, so do the cross product of the vectors find the direction of the product based on the sign.

Formula used:
If $\widehat i,\widehat j,\widehat k$ are the unit vectors along $x,y,z$ axis respectively, then one of the relations between the unit vectors related to cross multiplications is :
$\widehat j \times \widehat k = \widehat i$
$ \Rightarrow \widehat k \times \widehat j = - \widehat i$

Complete step by step answer:
A vector $\overrightarrow A $ is along vertically upward and another vector $\overrightarrow B $ is along the north direction. If this is drawn in a plane of a paper it looks like:

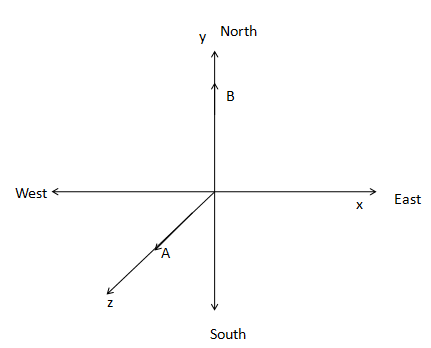
$\overrightarrow A $is along the $z$ axis that is along the normal direction to the plane of the paper. $\overrightarrow B $ is along the $y$ axis that is along the north direction to the plane.
If $\widehat i,\widehat j,\widehat k$ are the unit vectors along the positive $x,y,z$ axis respectively, then
\[\overrightarrow A = A\widehat k\]
And, \[\overrightarrow B = B\widehat j\]
We know, one of the relations between the unit vectors related to cross multiplications is :
$\widehat j \times \widehat k = \widehat i$
$ \Rightarrow \widehat k \times \widehat j = - \widehat i$
Hence, $\overrightarrow A \times \overrightarrow B = A\widehat k \times B\widehat j = AB( - \widehat i)$
$\therefore \overrightarrow A \times \overrightarrow B = - AB\widehat i$
Since the unit vector is $\widehat i$ with a negative sign, the resultant vector will be along the negative $x$ axis. From the figure it can be seen that the negative $x$ axis is directed towards the west direction.

Hence the correct option is (B).

Note: $\widehat i,\widehat j,\widehat k$ are the unit vectors along the positive $x,y,z$ axis respectively. Each of them has a value $1$ .
Since $\overrightarrow A \times \overrightarrow A = 0$ ;
Hence, $\widehat i \times \widehat i = \widehat j \times \widehat j = \widehat k \times \widehat k = 0$ .
Again, the value of $\widehat i \times \widehat j = \left| {\widehat i \times \widehat j} \right| = \left( 1 \right).\left( 1 \right).\sin {90^ \circ } = 1$
The rule of right hand cork-screw, the direction of $\widehat i \times \widehat j$ is along the $z$ axis. Since $\widehat k$ is the unit vector along the $z$ axis, so $\widehat i \times \widehat j = \widehat k$
According to this rule, $\widehat i \times \widehat j = \widehat k$, $\widehat j \times \widehat k = \widehat i$ and, \[\widehat k \times \widehat i = \widehat j\]
Since, $\overrightarrow A \times \overrightarrow B = - \overrightarrow B \times \overrightarrow A $
Hence, $\widehat j \times \widehat i = - \widehat k$, $\widehat k \times \widehat j = - \widehat i$ and, \[\widehat i \times \widehat k = - \widehat j\]