
Airspeed of an aeroplane is 400km/hr. The wind is blowing at 200km/hr towards the east direction. In what direction should the pilot try to fly the plane to move exactly towards the northeast.
Answer
133.8k+ views
Hint: When the plane is moving and the wind is blowing due east in this situation when the plane steers towards northeast then the effect of wind blowing will also affect the angle turned by the aeroplane it will turn more than it was steered to turn. So, if we want to steer at a particular angle then we need to steer at an angle lower than desired because the rest of the turn will be due to the effect of wind.
Complete step by step solution:
Consider the following diagram in this case: the plane is flying and the wind is blowing due east. Now here it is said that the plane needs to be steered exactly northeast. Now as we can see that the exact northeast will be at
So if we need to travel at
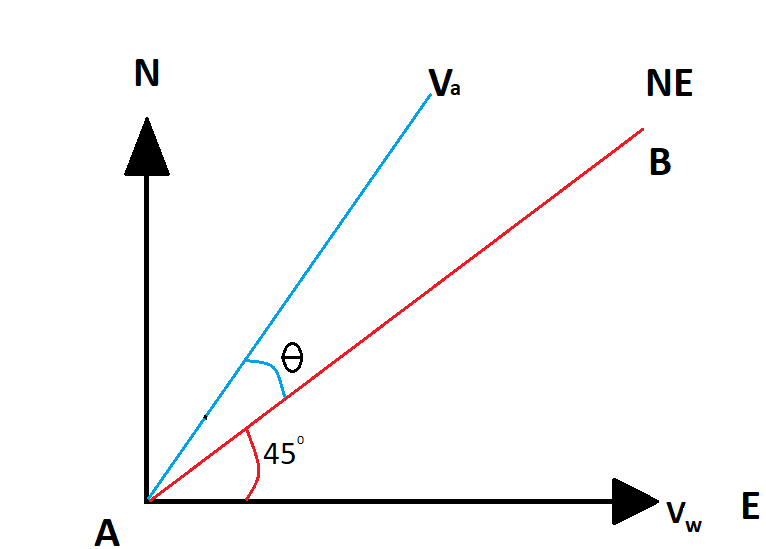
Now in this figure, the red line is the actual path the plane needs to turn and the blue line is the path we will turn to compensate for the effect of wind blowing due east.
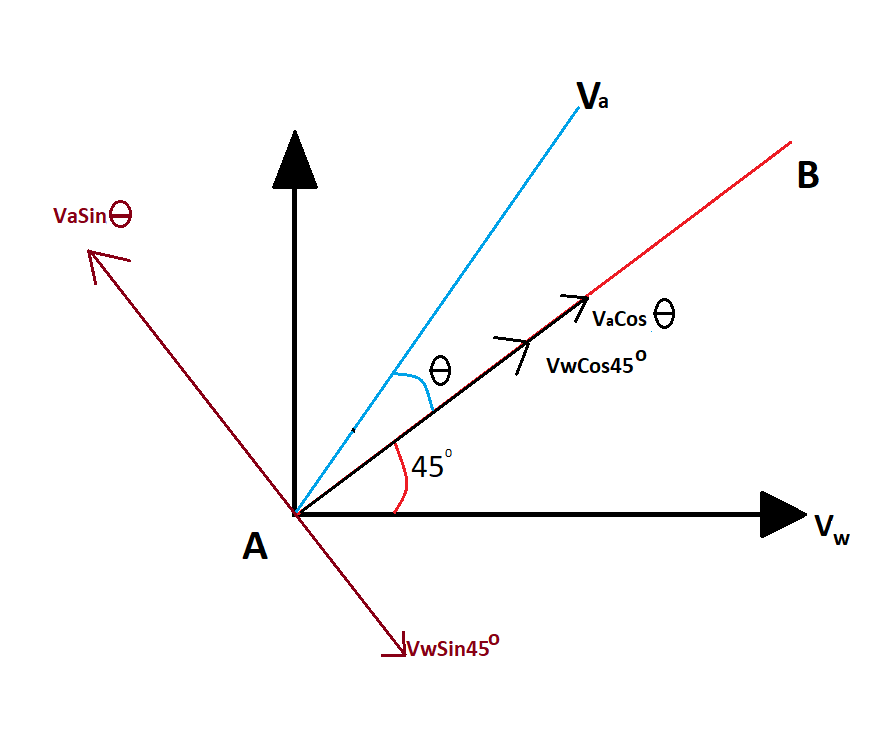
Now resolving the components of
And
Similarly,
Now we will resolve
So, we will get
And
Now in the figure, we can see that the components
And
So the net resultant force will be along AB and plane will steer exactly at
On equating we get
Substituting the values, we get
Final answer: The pilot needs to turn an angle of
Note: The resultant of both the motion will give us the actual motion.
When a plane is flying and it takes a turn and there is wind flowing then the effect of the wind will also be considered in steering the plane.
The effect of wind generally increases or decreases the angle the pilot needs to steer the plan to get into a particular direction.
Complete step by step solution:
Consider the following diagram in this case: the plane is flying and the wind is blowing due east. Now here it is said that the plane needs to be steered exactly northeast. Now as we can see that the exact northeast will be at
So if we need to travel at

Now in this figure, the red line is the actual path the plane needs to turn and the blue line is the path we will turn to compensate for the effect of wind blowing due east.

Now resolving the components of
And
Similarly,
Now we will resolve
So, we will get
And
Now in the figure, we can see that the components
And
So the net resultant force will be along AB and plane will steer exactly at
On equating we get
Substituting the values, we get
Final answer: The pilot needs to turn an angle of
Note: The resultant of both the motion will give us the actual motion.
When a plane is flying and it takes a turn and there is wind flowing then the effect of the wind will also be considered in steering the plane.
The effect of wind generally increases or decreases the angle the pilot needs to steer the plan to get into a particular direction.
Recently Updated Pages
JEE Main 2025 Session 2 Form Correction (Closed) – What Can Be Edited

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main Books 2023-24: Best JEE Main Books for Physics, Chemistry and Maths

JEE Main 2023 April 13 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 11 Shift 2 Question Paper with Answer Key

JEE Main 2023 April 10 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Class 11 JEE Main Physics Mock Test 2025

JEE Main Chemistry Question Paper with Answer Keys and Solutions

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion In A Plane: Line Class 11 Notes: CBSE Physics Chapter 3




