Question

An ammeter having resistance ${R_0}$ shows full deflection when the current $I$ flow from it. What resistance should be connected to it in series so that it shows deflection $\dfrac{I}{n}$ when the same current flows.
A) $\dfrac{{{R_0}}}{n}$
B) ${R_0}\left( {n - 1} \right)$
C) $\dfrac{{{R_0}}}{{n + 1}}$
D) None of these

Answer 1

Hint: To solve this question, we have to understand the arrangement in which a galvanometer can be converted to an ammeter. To convert a galvanometer to ammeter, a resistor of very low resistance called shunt resistance should be connected in parallel to the galvanometer.

Complete step by step solution:
An ammeter is a device used to measure the magnitude of current flowing through the wire. It is connected in the series with the branch in which current has to be measured.
An ammeter can be constructed from a galvanometer by connecting a low resistance in parallel to the galvanometer as shown:

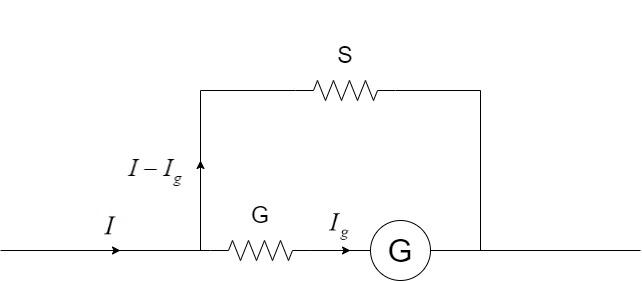
If G is the resistance of the galvanometer, $I$ is the current to be measured and ${I_g}$ is the current flowing through the galvanometer, the value of shunt resistance connected to the galvanometer is given by –
$S = \dfrac{{G{I_g}}}{{I - {I_g}}}$
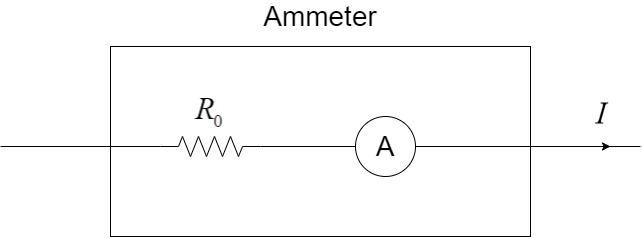
Thus, the complete setup can be summarised as the schematic figure of an ammeter with a resistance which is given here, as ${R_0}$ with the current I flowing through the ammeter.

Let R be another resistance connected in series with ${R_0}$ such that the current flowing through the ammeter shall be $\dfrac{I}{n}$ as shown:

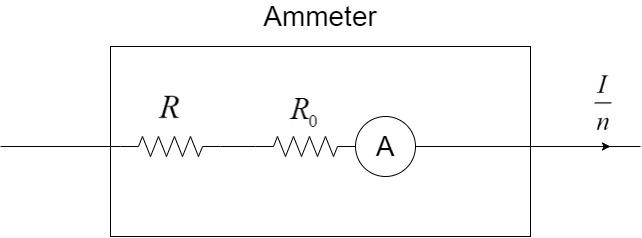
In both the cases, the voltage drop across the ammeter remains constant since the current flowing is the same in both the cases.
Voltage drop in the first case: $V = I{R_0}$
Voltage drop in the second case: $V = \dfrac{I}{n}\left( {R + {R_0}} \right)$
Equating them, we get –
$I{R_0} = \dfrac{I}{n}\left( {R + {R_0}} \right)$
$ \Rightarrow {R_0} = \dfrac{{R + {R_0}}}{n}$
$ \Rightarrow n{R_0} = R + {R_0}$
$ \Rightarrow R = n{R_0} - {R_0}$
$ \Rightarrow R = {R_0}\left( {n - 1} \right)$

Hence, the correct option is Option B.

Note: The students must note the fact that in an ammeter, the shunt resistor used, has a very low value, usually in micro- or milli- ohms. If you encounter any problem on calculating the shunt resistance in an ammeter and you do not get a low resistance, it is sure that the solution is headed in the wrong direction.