
An electron, a proton, a deuteron, and an alpha particle, each having speed are in a region of constant magnetic field perpendicular to the direction of the velocities of the particles. The radius of the circular orbits of these particles is respectively ${{R}_{e,}}{{R}_{p}},{{R}_{d}}$and ${{R}_{\alpha }}$. It follows that
A. ${{R}_{e}}={{R}_{p}}$
B.${{R}_{p}}={{R}_{d}}$
C.${{R}_{d}}={{R}_{\alpha }}$
D.${{R}_{p}}={{R}_{\alpha }}$
Answer
219.3k+ views
Hint: When a charged particle moves with definite velocity and enters a uniform magnetic field $B$, then it experiences a magnetic force perpendicular to the direction of motion and it travels a circular path. Then by equating magnetic force with centripetal force, we can derive the equation of the radius of a circular path.
Formula used:
The radius,$R$ of the circular path in a magnetic field,$B$can be expressed in the following way:
$R=\dfrac{mv}{qB}$
Here $m\And v$are the mass and velocity of the particle with charge $q$.
Complete answer:
When a particle carrying charge$q$, moving with velocity $\vec{v}$enters into a magnetic field $\vec{B}$, it experiences a magnetic force, $\vec{F}=q(\vec{B}\times \vec{v})$
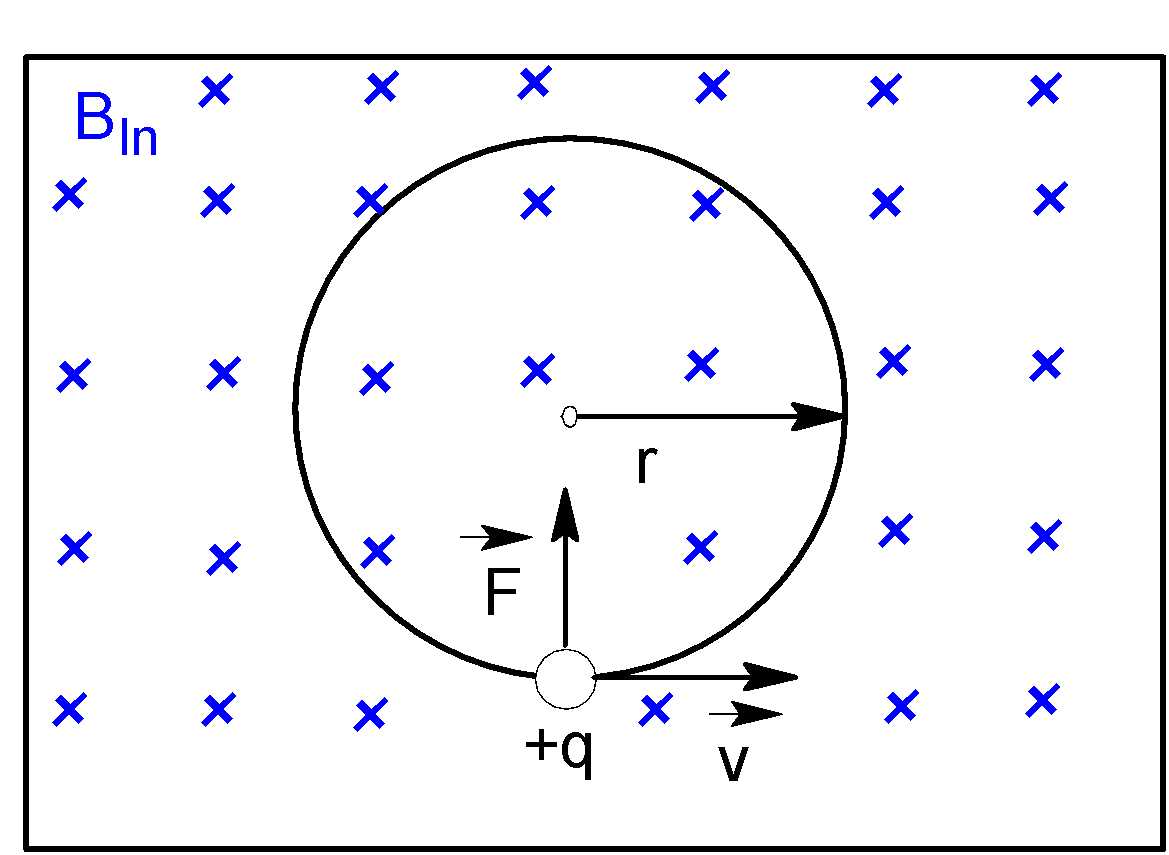
Or,$F=q(Bv\sin {{90}^{o}})$ [Since $\vec{B}$is perpendicular to $\vec{v}$]
Or,$F=qBv$ ……..(i)
As a particle moves in a circular path, then magnetic force becomes a centripetal force $\dfrac{m{{v}^{2}}}{R}$.
Hence by equating magnetic force with centripetal force,
$qBv=\dfrac{m{{v}^{2}}}{R}$
Or,$R=\dfrac{mv}{qB}$
Here we have four charged particles: an electron($e$), a proton ($p$), a deuteron ($d$), and an alpha particle $(\alpha )$. They all have equal speed,$v$and move in a region of the constant magnetic field,$B$.
Therefore the radius of the circular path mainly depends on $\dfrac{mass(m)}{ch\arg e(q)}$ratio.
Or,$R$ $\alpha $ $\dfrac{m}{q}$
Let us check $\dfrac{m}{q}$ratio of each charged particle in the following table,
Let the Mass of a proton be $m$and charge $q$.
As we know the mass of an electron, deuterium and an alpha particle are $\dfrac{1}{1836}$, $2$ and $4$ times the mass of the proton.
Therefore $\dfrac{m}{q}$ ratio for deuterium and an alpha particle are equal, hence their radius of the circular orbit would be equal i.e,${{R}_{d}}={{R}_{\alpha }}$.
Thus, option (C) is correct.
Note:Neutron does not feel any magnetic force while other charged particles experience that force. A neutron is a neutral particle, having no charge. But for charged particle trajectory curvature is proportional to the mass by charge ratio for a definite velocity.
Formula used:
The radius,$R$ of the circular path in a magnetic field,$B$can be expressed in the following way:
$R=\dfrac{mv}{qB}$
Here $m\And v$are the mass and velocity of the particle with charge $q$.
Complete answer:
When a particle carrying charge$q$, moving with velocity $\vec{v}$enters into a magnetic field $\vec{B}$, it experiences a magnetic force, $\vec{F}=q(\vec{B}\times \vec{v})$

Or,$F=q(Bv\sin {{90}^{o}})$ [Since $\vec{B}$is perpendicular to $\vec{v}$]
Or,$F=qBv$ ……..(i)
As a particle moves in a circular path, then magnetic force becomes a centripetal force $\dfrac{m{{v}^{2}}}{R}$.
Hence by equating magnetic force with centripetal force,
$qBv=\dfrac{m{{v}^{2}}}{R}$
Or,$R=\dfrac{mv}{qB}$
Here we have four charged particles: an electron($e$), a proton ($p$), a deuteron ($d$), and an alpha particle $(\alpha )$. They all have equal speed,$v$and move in a region of the constant magnetic field,$B$.
Therefore the radius of the circular path mainly depends on $\dfrac{mass(m)}{ch\arg e(q)}$ratio.
Or,$R$ $\alpha $ $\dfrac{m}{q}$
Let us check $\dfrac{m}{q}$ratio of each charged particle in the following table,
Let the Mass of a proton be $m$and charge $q$.
| Proton | Electron | deuteron | deuteron | |
| Mass($m$) | $m$ | $\dfrac{m}{1836}$ | $2m$ | $4m$ |
| Charge($q$) | $q$ | $q$ | $q$ | $2q$ |
| $\dfrac{mass}{ch\arg e}\left( \dfrac{m}{q} \right)$ | $\dfrac{m}{q}$ | $\dfrac{m}{q\times 1836}$ | $\dfrac{2m}{q}$ | $\dfrac{4m}{2q}=\dfrac{2m}{q}$ |
As we know the mass of an electron, deuterium and an alpha particle are $\dfrac{1}{1836}$, $2$ and $4$ times the mass of the proton.
Therefore $\dfrac{m}{q}$ ratio for deuterium and an alpha particle are equal, hence their radius of the circular orbit would be equal i.e,${{R}_{d}}={{R}_{\alpha }}$.
Thus, option (C) is correct.
Note:Neutron does not feel any magnetic force while other charged particles experience that force. A neutron is a neutral particle, having no charge. But for charged particle trajectory curvature is proportional to the mass by charge ratio for a definite velocity.
Recently Updated Pages
A square frame of side 10 cm and a long straight wire class 12 physics JEE_Main

The work done in slowly moving an electron of charge class 12 physics JEE_Main

Two identical charged spheres suspended from a common class 12 physics JEE_Main

According to Bohrs theory the timeaveraged magnetic class 12 physics JEE_Main

ill in the blanks Pure tungsten has A Low resistivity class 12 physics JEE_Main

The value of the resistor RS needed in the DC voltage class 12 physics JEE_Main

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Understanding Uniform Acceleration in Physics

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

How to Convert a Galvanometer into an Ammeter or Voltmeter

Understanding Centrifugal Force in Physics

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Degree of Dissociation: Meaning, Formula, Calculation & Uses




