Question

An equilateral triangle of side $a$ carries a current $I$. What is the magnitude and direction of the magnetic field at the point $P$?

Answer 1

Hint: First, we have to know about the magnetic field and how it can be generated from electricity. We can determine the magnetic field's magnitude thus produced if we know about the correlation between the electric field and the magnetic field. After that, we can find out the direction of the generated magnetic field with the right-hand rule.

Formula used:
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$

Complete step by step solution:
The vector field that describes the magnetic influence on moving electric charges or electric current or any other magnetic material is known as the magnetic field. A current-carrying wire can produce a magnetic field in its surroundings. The right-hand rule can determine the direction of the magnetic field. The correlation of the current and the produced magnetic field can be given as-
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$
where,
$B$ is the magnitude of the magnetic field
$I$ is the current flowing through the conductor
${\mu _0}$ is the magnetic permittivity of vacuum
$r$ is the distance from the conductor to the point of the magnetic field
However, here, we will think more deeply and use symmetry to solve our problem.
So the sides $PQ$ and $PR$ do not contribute to the generation of the magnetic field at $P$.

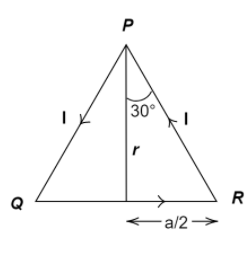
Here,
$\Rightarrow r = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \sqrt {{a^2} - \dfrac{{{a^2}}}{4}} $
Upon solving further we get,
$\Rightarrow r = \sqrt {\dfrac{{3{a^2}}}{4}} $
$ \Rightarrow r = \dfrac{{\sqrt 3 a}}{2}$
Therefore,
$\Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}.\dfrac{I}{r}\left[ {\sin {\alpha _1} + \sin {\alpha _2}} \right]$
We put ${\alpha _1} = {\alpha _2} = {30^ \circ }$ , and we get-
$\Rightarrow B = \dfrac{{{\mu _0}}}{{4\pi }}.\dfrac{I}{{\left( {\dfrac{{\sqrt 3 a}}{2}} \right)}}\left[ {\sin \left( {{{30}^ \circ }} \right) + \sin \left( {{{30}^ \circ }} \right)} \right]$
We put $\sin \left( {{{30}^ \circ }} \right) = \dfrac{1}{2}$-
$\Rightarrow B = \dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}}\left[ {\dfrac{1}{2} + \dfrac{1}{2}} \right]$
$ \Rightarrow B = \dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}}$
Hence, the magnitude of the generated magnetic field is $\dfrac{{{\mu _0}I}}{{2\sqrt 3 \pi a}}$ , and with the right-hand rule, we can determine that the magnetic field's direction is upward, i.e., pointing outward of the page.

Note: In this problem, we have used the Biot-Savart Law to determine the magnetic field. We will always use the Biot-Savart Law to solve problems where we can use symmetry to find out the magnetic field generated due to the action of a current-carrying conductor.