
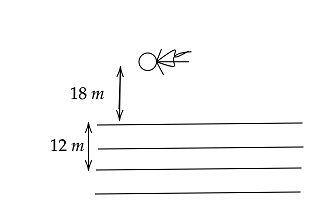
An underwater swimmer is at a depth of \[12\,m\] below the surface of water. A bird is at a height of $18\,m$ from the surface of water, delivery above his eyes. for the swimmer the birds appear to be at a distance from the surface of water equal to (refractive index of water is $4/3$)
(A) $24\,m$
(B) $12\,m$
(C) $18\,m$
(D) $\,9m$
Answer
129k+ views
Hint Here we know that the bird's underwater depth and height value also know the refractive index value so that we calculate the width of the water above the depth is referred to as the refractive index. By using the definition of the velocity in a medium.
Complete step by step answer
Given by,
Height of bird from surface of water $ = 18m$
Depth of swimmer below the surface of water $ = 12m$(Real depth)
Refractive index of water $ = 4/3$
We have to find apparent depth of swimmer
Apparent depth in a medium is the depth of an object in a denser medium as seen from the rarer medium.
Its value is smaller than the real depth.
The bird lies in Air medium and the observer is the swimmer which lies in water.
So that,
Refractive index of water $\mu = \dfrac{4}{3}$
Apparent depth can be calculated by using this formula
\[\mu = \dfrac{{real\,height}}{{apparent\,height}}\]
Substituting the given value in above equation,
We get,
$\dfrac{4}{3} = \dfrac{{real\,depth}}{{18}}$
Rearranging the given equation,
$real\,height = \dfrac{4}{3} \times 18$
On simplifying the above equation,
$real\,height = 24\,m$
Hence,
$24\,m$ above surface of water
Thus, option A is correct answer.
Note According to the above definition, there is a different refractive index as it moves at an angle towards a medium. Similarly, the light ray moves obliquely in the air entering the water, the light ray bends towards the normal, because water as a medium has an optically denser medium than air. This shift in speed results in a change in direction.
Complete step by step answer
Given by,
Height of bird from surface of water $ = 18m$
Depth of swimmer below the surface of water $ = 12m$(Real depth)
Refractive index of water $ = 4/3$
We have to find apparent depth of swimmer
Apparent depth in a medium is the depth of an object in a denser medium as seen from the rarer medium.
Its value is smaller than the real depth.
The bird lies in Air medium and the observer is the swimmer which lies in water.
So that,

Refractive index of water $\mu = \dfrac{4}{3}$
Apparent depth can be calculated by using this formula
\[\mu = \dfrac{{real\,height}}{{apparent\,height}}\]
Substituting the given value in above equation,
We get,
$\dfrac{4}{3} = \dfrac{{real\,depth}}{{18}}$
Rearranging the given equation,
$real\,height = \dfrac{4}{3} \times 18$
On simplifying the above equation,
$real\,height = 24\,m$
Hence,
$24\,m$ above surface of water
Thus, option A is correct answer.
Note According to the above definition, there is a different refractive index as it moves at an angle towards a medium. Similarly, the light ray moves obliquely in the air entering the water, the light ray bends towards the normal, because water as a medium has an optically denser medium than air. This shift in speed results in a change in direction.
Recently Updated Pages
The probability density function pleft x right cannot class 9 maths JEE_Main

What are the products formed when moist chlorine gas class 9 chemistry JEE_Main

The weight of a fruit bun Nisha bought was equal to class 9 maths JEE_Main

Ansgar is writing a novel He writes seven days a week class 9 maths JEE_Main

A college offers 7 courses in the morning and 5 in class 9 maths JEE_Main

Add the following algebraic expression using both horizontal class 9 maths JEE_Main

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

Degree of Dissociation and Its Formula With Solved Example for JEE

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Mains 2025 Correction Window Date (Out) – Check Procedure and Fees Here!

Electromagnetic Waves Chapter - Physics JEE Main

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Diffraction of Light - Young’s Single Slit Experiment

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Wheatstone Bridge for JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation




