
Add the following algebraic expression using both horizontal and vertical methods.
Did you get the same answer with both methods?
$2{x^2} - 6x + 3; - 3{x^2} - x + 4;1 + 2x - 3{x^2}$
Answer
133.2k+ views
Hint: The horizontal method and the vertical method of adding the expression are two different ways to add the expression but the resultant answer is the same in both the cases.
Complete step-by-step answer:
Given algebraic expressions are $2{x^2} - 6x + 3; - 3{x^2} - x + 4;1 + 2x - 3{x^2}$
Assume the given algebraic expression as the functions:
$f\left( x \right) = 2{x^2} - 6x + 3$ ,
$g\left( x \right) = - 3{x^2} - x + 4$
$h\left( x \right) = 1 + 2x - 3{x^2}$
First, we add these expressions using the horizontal method. In the horizontal method of adding the expression, we first need to write all the expression in a horizontal line and then make groups of like terms, after that add all the like terms together.
$S\left( x \right) = f\left( x \right) + g\left( x \right) + h\left( x \right)$
Substitute $2{x^2} - 6x + 3$as the value of$f\left( x \right)$, $ - 3{x^2} - x + 4$as the value of$g\left( x \right)$and $1 + 2x - 3{x^2}$as the value of $h\left( x \right)$in the above expression:
$S\left( x \right) = \left( {2{x^2} - 6x + 3} \right) + \left( { - 3{x^2} - x + 4} \right) + \left( {1 + 2x - 3{x^2}} \right)$
Open the braces and express the terms:
$S\left( x \right) = 2{x^2} - 6x + 3 - 3{x^2} - x + 4 + 1 + 2x - 3{x^2}$
Now, collect all the like terms together and add them.
$S\left( x \right) = 2{x^2} - 3{x^2} - 3{x^2} - 6x - x + 2x + 3 + 4 + 1$
$S\left( x \right) = 4{x^2} - 5x + 8$
The sum of the given expression using the horizontal method is$4{x^2} - 5x + 8$.
Now, add the functions in the vertical method. In this method of adding expression, we first need to arrange the expressions in a vertical line in such a manner that the like terms and their signs are one below the other, and then add them.
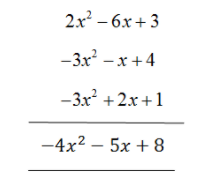
The sum of the given expression using the vertical method is$4{x^2} - 5x + 8$.
When we added the given expression using the horizontal method, then we have the solution:
$4{x^2} - 5x + 8$
And when we added the given expression using the vertical method, then we have the solution:
$4{x^2} - 5x + 8$
It can be seen that both solutions are the same. The conclusion is that we get the same answer using horizontal and vertical methods both.
Note: The like terms are the terms of the expression that have the same variables raised to the same power. In the given expressions, $2{x^2} - 6x + 3; - 3{x^2} - x + 4;1 + 2x - 3{x^2}$, the like terms are $\left( {2{x^2}, - 3{x^2}, - 3{x^2}} \right),\left( { - 6x, - x,2x} \right){\text{ and }}\left( {3,4,1} \right)$.
Complete step-by-step answer:
Given algebraic expressions are $2{x^2} - 6x + 3; - 3{x^2} - x + 4;1 + 2x - 3{x^2}$
Assume the given algebraic expression as the functions:
$f\left( x \right) = 2{x^2} - 6x + 3$ ,
$g\left( x \right) = - 3{x^2} - x + 4$
$h\left( x \right) = 1 + 2x - 3{x^2}$
First, we add these expressions using the horizontal method. In the horizontal method of adding the expression, we first need to write all the expression in a horizontal line and then make groups of like terms, after that add all the like terms together.
$S\left( x \right) = f\left( x \right) + g\left( x \right) + h\left( x \right)$
Substitute $2{x^2} - 6x + 3$as the value of$f\left( x \right)$, $ - 3{x^2} - x + 4$as the value of$g\left( x \right)$and $1 + 2x - 3{x^2}$as the value of $h\left( x \right)$in the above expression:
$S\left( x \right) = \left( {2{x^2} - 6x + 3} \right) + \left( { - 3{x^2} - x + 4} \right) + \left( {1 + 2x - 3{x^2}} \right)$
Open the braces and express the terms:
$S\left( x \right) = 2{x^2} - 6x + 3 - 3{x^2} - x + 4 + 1 + 2x - 3{x^2}$
Now, collect all the like terms together and add them.
$S\left( x \right) = 2{x^2} - 3{x^2} - 3{x^2} - 6x - x + 2x + 3 + 4 + 1$
$S\left( x \right) = 4{x^2} - 5x + 8$
The sum of the given expression using the horizontal method is$4{x^2} - 5x + 8$.
Now, add the functions in the vertical method. In this method of adding expression, we first need to arrange the expressions in a vertical line in such a manner that the like terms and their signs are one below the other, and then add them.
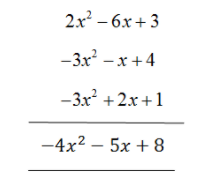
The sum of the given expression using the vertical method is$4{x^2} - 5x + 8$.
When we added the given expression using the horizontal method, then we have the solution:
$4{x^2} - 5x + 8$
And when we added the given expression using the vertical method, then we have the solution:
$4{x^2} - 5x + 8$
It can be seen that both solutions are the same. The conclusion is that we get the same answer using horizontal and vertical methods both.
Note: The like terms are the terms of the expression that have the same variables raised to the same power. In the given expressions, $2{x^2} - 6x + 3; - 3{x^2} - x + 4;1 + 2x - 3{x^2}$, the like terms are $\left( {2{x^2}, - 3{x^2}, - 3{x^2}} \right),\left( { - 6x, - x,2x} \right){\text{ and }}\left( {3,4,1} \right)$.
Recently Updated Pages
Difference Between Mutually Exclusive and Independent Events

Difference Between Area and Volume

Difference Between Double Salt and Complex Salt: JEE Main 2024

JEE Main 2025: What is the Area of Square Formula?

Difference Between Power and Exponent: JEE Main 2024

Difference Between Pound and Kilogram with Definitions, Relation

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

JEE Main Syllabus 2025 (Updated)

JEE Mains 2025 Cutoff: Expected and Category-Wise Qualifying Marks for NITs, IIITs, and GFTIs

Raoult's Law with Examples

JEE Main Marks Vs Percentile Vs Rank 2025: Calculate Percentile Using Marks

How Many Students Will Appear in JEE Main 2025?

Other Pages
NCERT Solutions for Class 9 Maths Chapter 11 Surface Area and Volume

NCERT Solutions for Class 9 Maths Chapter 11 Surface Areas And Volumes Ex 11.3

NCERT Solutions for Class 9 Maths Chapter 9 Circles

NCERT Solutions for Class 9 Maths Chapter 12 Statistics

NCERT Solutions for Class 9 Maths Chapter 10 Heron'S Formula

NCERT Solutions for Class 9 Maths In Hindi Chapter 1 Number System





