Question

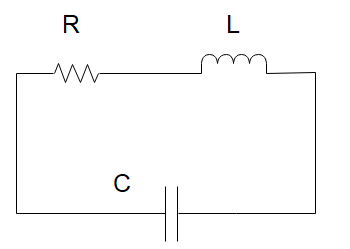
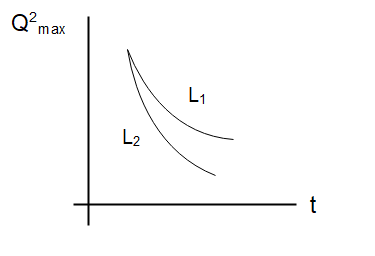
An LCR circuit is equivalent to a damped pendulum. In an LCR circuit, the capacitor is charged to ${Q_0}$ and then connected to the L and R as shown above. If a student plots graphs of the square of maximum charge \[Q_{\max }^2\]on the capacitor with time (t) for two different values \[{L_1}\,\;{\text{and}}\;{L_2}\]\[\left( {{L_1}\, > {L_2}} \right)\] of $L$ then which of the following represents this graph correctly? (plots schematic and not drawn to scale)

(A)

(B)

(C)

(D)

Answer 1

Hint: In this solution, we will use the properties of the damped pendulum to determine the charge on the capacitor. The LCR circuit will be equivalent to a spring-mass-dashpot system without any external driving force acting on it.

Formula used: In this question, we will use the following formula
$Q = {Q_0}{e^{ - Rt/2L}}$ where $Q$ is the maximum change in an LCR circuit where ${Q_0}$ is the maximum charge in a capacitor, $R$ is the resistance, and $L$ is the inductance.

Complete step by step answer:
We know that anLCR circuit is equivalent to a damped pendulum and in the question we’ve been told that the capacitor is charged to ${Q_0}$ and then connected to the $L$ and $R$. This system is equivalent to a spring-mass dashpot system. In this system, we have a block that is oscillating connected to a spring and a dashpot. The purpose of the dashpot is to exert friction force on the mass in the system. The drag force exerted by the dashpot will be proportional to the velocity of the mass.
In the spring-mass dashpot case, the amplitude of the block $x$ is defined as a function of time as
$x = {x_0}{e^{ - t/\tau }}$. Here ${x_0}$ is the amplitude of the block, $t$ is the time , $\tau $is the characteristic damping time which depends on the dashpot.
Similarly, the charge on the capacitor as a function of time is given as
$Q = {Q_0}{e^{ - Rt/2L}}$
This is the charge on the capacitor. The behaviour of this graph is such that it exponentially decays with time. The inductor in an LCR circuit acts as the inertia of the circuit. This implies that the higher the inductance of the circuit, the slower the charge decay will be. So as ${L_1} > {L_2}$ has been given to us the charge in ${L_1}$ the circuit will decay slower than the charge in the circuit ${L_2}$

So, option (A) is the correct choice.

Note: To answer this question, we don’t necessarily need to know the properties of the damped oscillation system but since an LCR circuit is very similar, we can use its properties to determine the possible graph of the charge in the circuit.