Question

What is the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$.
A. $\dfrac{1}{2}$
B. $1$
C. $\dfrac{3}{2}$
D. $2$

Answer 1

Hint: To find the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$,we will write the value of $x$ in the given interval and determine the equation of the curve.
Then we will integrate it using limits by taking lower limit $x=0$ and upper limit $x=1$and determine the area.



Formula Used:The limits of integration of a function can be calculated by $\begin{align}
  & \int\limits_{b}^{a}{f(x).dx}=\left[ f(x) \right]_{b}^{a} \\
 & =f(a)-f(b)
\end{align}$



Complete step by step solution:We are given an equation of curve$y=|x|+|x-1|$ and we have to find the area enclosed by it in between the interval $x=0$ and $x=1$.
For the interval\[x\ge 0\],
$|x|=x$
And for the interval \[x\le 1\],
$|x-1|=-(x-1)$
The equation will be $y=x-(x-1)$
Now we will integrate it taking $x=0$as lower limit and $x=1$as upper limit.
\[Area=\int\limits_{0}^{1}{x.dx}-\int\limits_{0}^{1}{(x-1)dx}\]
\[=\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{1}-\left[ \dfrac{{{x}^{2}}}{2}-x \right]_{0}^{1}\]
Applying the limits,
\[=\left[ \dfrac{1}{2}-\dfrac{0}{2} \right]-\left[ \left( \dfrac{1}{2}-1 \right)-\left( \dfrac{0}{2}-0 \right) \right]\]
\[=\dfrac{1}{2}-\left( \dfrac{1}{2}-1 \right)\]
\[=1\]square unit.
The area under the curve $y=|x|+|x-1|$ between $x=0$ and $x=1$ is $1$ square units.
Thus, the area under the curve $y=|x|+|x-1|$ between$x=0$ and $x=1$



Option ‘D’ is correct

Note:We can also find the area under the curve by another method. In this method we will simplify the equation of the curve first.

The equation of the curve is .
Now we will draw the graph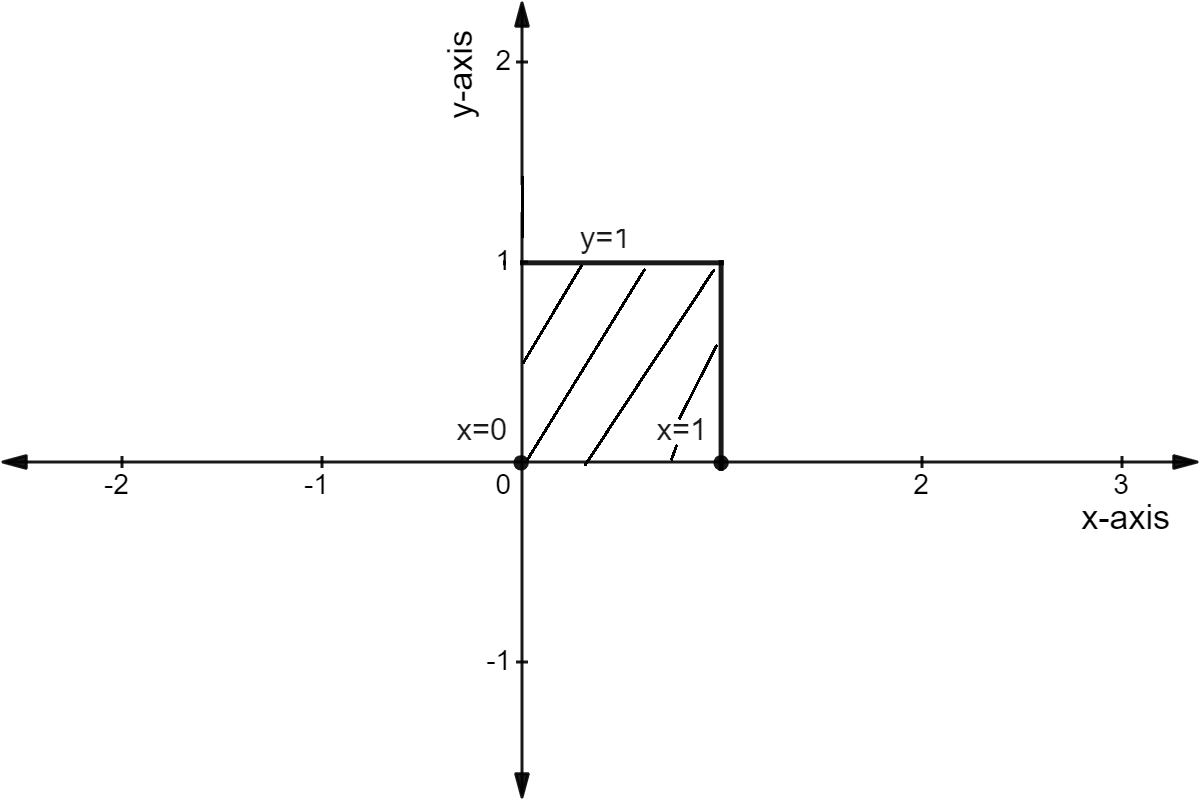

 We can see that a quadrilateral is formed on the graph of the curve between the interval l and . The quadrilateral formed is a square because each of the side is of length of unit .
We will calculate the area under the curve by finding the area of the square. As we know the formula of the area of the square is , we will use it.

 1 square units.
.