Question

As shown in the below figure a variable rheostat of $2k\Omega $ is used to control the potential difference across a $500$ ohm load.
(1). If the resistance $AB$ is $500\Omega $. What is the potential difference across loads?
(2). If the load is removed, what should be the resistance of $BC$ to get $40$ Volt between B q C ?

Answer 1

Hint: Resistance: It is the property of any material which obstructs the flow of current.
Resistance in parallel: Two resistors when connected in parallel then the current through each resistor is different and potential difference across $\left( V \right)$ Each resistor remains the same. The equivalent resistance of two resistor connected parallel is.
$\dfrac{1}{{{R_P}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} = \dfrac{{{R_2} + {R_1}}}{{{R_1}{R_2}}}$
Then ${R_P} = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}$
Resistances in series: Two or more resistors are said to be connected in series if they are connected end to end and current flows through each resistor is the same.
The equivalent resistance between $AB$ is
${R_S} = {R_1} + {R_2}$
Ohm’s Law: According to ohm’s law
$V = IR$
$R = \dfrac{V}{I}$

Complete step by step answer:
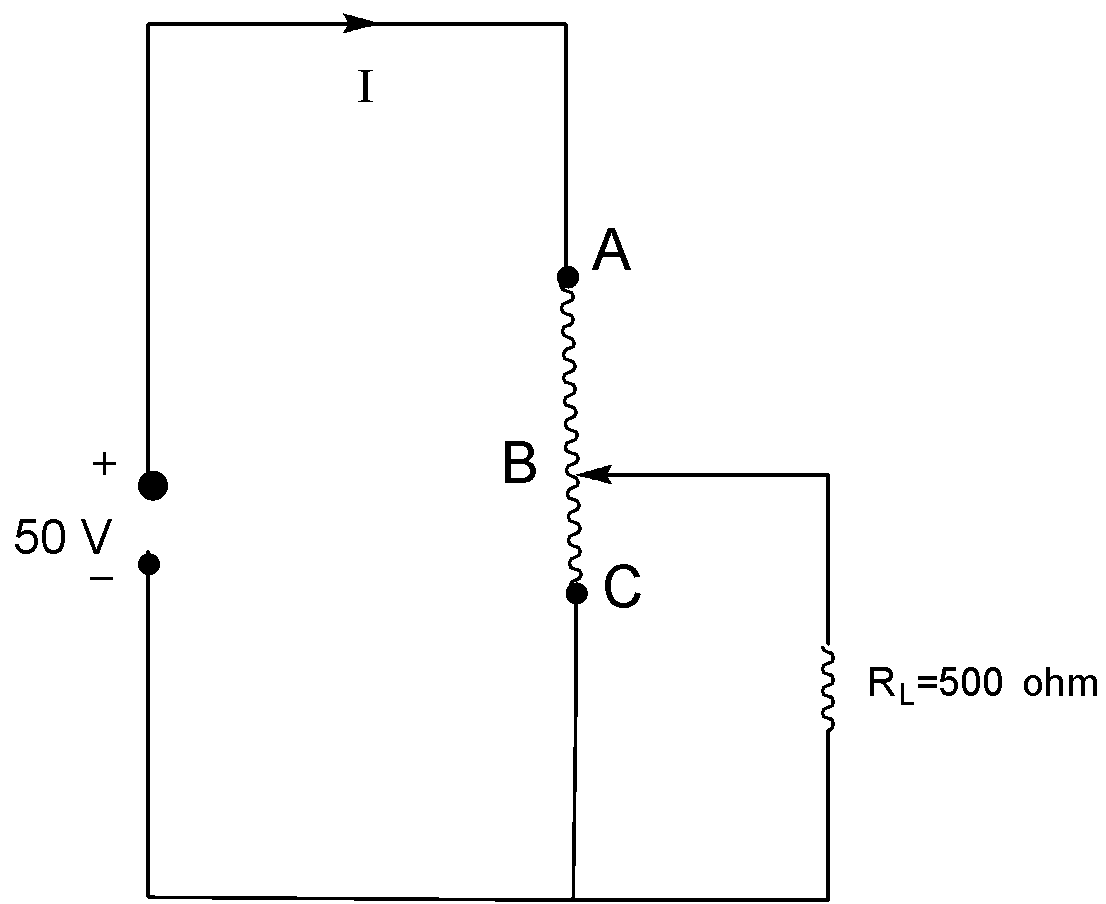
Step.1 Given
Resistance across $AC = {R_{AC}} = 2K\Omega = 2000\Omega $
$1{\text{ kilo ohm = 1000 ohm}}$
Load resistance $\left( {{R_L}} \right) = 500\Omega $
Resistance across $AB\left( {{R_{AB}}} \right) = 500\Omega $
Now resistance across $BC$ is.
$\implies$ ${R_{BC}} = {R_{AC}} - {R_{AB}}$
Now put the value of ${R_{AC}}$ and ${R_{AB}}$ in above given equation
$\implies$ ${R_{BC}} = 2000 - 500 = 1500{\text{ ohm}}$
Now ${R_{BC}}$ and ${R_L}$ are in parallel combination.
So total resistance of the parallel combination of ${R_{BC}}$ and ${R_L}$ is
$\implies$ $R' = \dfrac{{1500 \times 500}}{{1500 + 500}} = \dfrac{{750000}}{{2000}} = 375\Omega $
$\implies$ $R' = 375$
Total resistance of the circuit is.
$\implies$ $R = {R_{AB}} + R'$
$\implies$ $R'$ is the resistance of the parallel combination of ${R_{AB}}{\text{ }}\& {\text{ }}{R_L}$.
$\implies$ $R = 500 + 375 = 875$
Now the current across the circuit is
By ohm’s law $V = IR$
$I = \dfrac{V}{R}$
$\implies$ $I = \dfrac{{50V}}{{875\Omega }} = \dfrac{2}{{35}}A$
$\implies$ $I = \dfrac{2}{{35}}A$
1. The potential drop across ${R_L}$ will be the same as the potential drop across $R'$ ( $R'$ is the parallel combination of ${R_{BC}}$ and ${R_L}$ )
Now,
Potential drop across ${R_L}$ is
$ = V - {V_{AB}}$
$\implies$ ${V_{AB}}$ = potential drop across $AB$
$\implies$ ${V_{AB}} = \dfrac{2}{{35}} \times 500$
Now we have
$ = 50 - \dfrac{2}{{35}} \times 500 = 50 - 28.57 = 21.43{\text{ V}}$
So potential drop across ${R_L} = 21.43{\text{ V}}$
2. If the load is removed then the entire current will flow through resistance ${R_{AC}}$ of the rheostat.
Now the current across the circuit is.
$I' = \dfrac{{50V}}{{2000\Omega }} = \dfrac{1}{{40}}A$
To obtain a potential drop of $40V$ between $B$ and $C$, then required resistance $BC$ must be
$\implies$ $R{'_{BC}} = \dfrac{{40V}}{{\dfrac{1}{{40}}A}} = 1600\Omega $
 $\implies$ $R{'_{BC}} = 1600\Omega $

Note:
In series resistance circuit it should be noted.
1. The current through all the resistors is the same.
2. The total resistance of the circuit is equal to the sum of individual resistances including internal resistance of the cell.
3. The potential difference across any resistor is proportional to its resistance.
 In a parallel resistance circuit it should be noted.
(1). The total current through parallel combination is equal to the sum of individual currents through the various resistors.
(2). The potential difference across all the resistors is the same.
(3). The current through any resistor is inversely proportional to its resistance.