Question

Assertion: Vector addition of two vectors A and B is commutative.
Reason:
\[\begin{array}{*{20}{c}}
  {\overrightarrow A + \overrightarrow B }& = &{\overrightarrow B + \overrightarrow A }
\end{array}\]
A) Both assertion and reason are correct and the reason is the correct explanation for the assertion.
B) Both assertion and reason are correct but Reason is not the correct explanation for the assertion.
C) Assertion is correct but Reason is incorrect.
D) Both assertion and reason are incorrect.

Answer 1

Hint:
In this question, we have given that the vectors A and B are commutative and according to the commutative law, if two vectors are added in any order, then the resultant of those vectors will be the same. And we will determine the addition of two vectors that are to be added in any order. And then we will select the correct answer from the given options.


Complete step by step solution:
Let us assume that there are two vectors \[\overrightarrow A \]and \[\overrightarrow B \]. And \[\overrightarrow R \] is the resultant vector. therefore, we will add these two vectors using the triangle law of vector addition.
The Triangle law of vector addition says that if two vectors show the side of the triangle, then the third side of the triangle shows the resultant of the vector having the magnitude and the direction.
Now we will add the vector \[\overrightarrow A \] and \[\overrightarrow B \]. Therefore, we will get

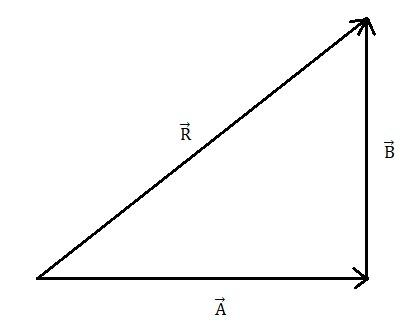
Figure 1
From figure - 1, we can write
\[ \Rightarrow \begin{array}{*{20}{c}}
  {\overrightarrow R }& = &{\overrightarrow A + \overrightarrow B }
\end{array}\]……….. (1)
And when we will add the vector \[\overrightarrow B \]and \[\overrightarrow A \], then we will get

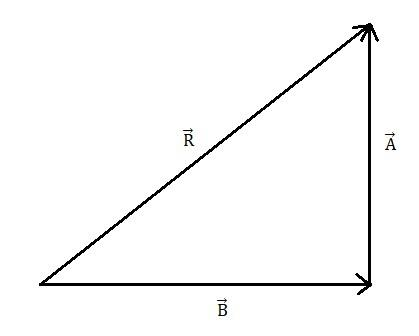
Figure 2
From figure - 2, we will get
\[ \Rightarrow \begin{array}{*{20}{c}}
  {\overrightarrow R }& = &{\overrightarrow B + \overrightarrow A }
\end{array}\] ……………… (2)
Now from the equation (1) and (2), we will get
\[ \Rightarrow \begin{array}{*{20}{c}}
  {\overrightarrow A + \overrightarrow B }& = &{\overrightarrow B + \overrightarrow A }
\end{array}\]
Therefore, the assertion is correct and the reason is also correct. But the reason is not the correct clarification for the assertion.
Therefore, the correct option is B.



Note:
In this question, we have given that the vector addition of the two vectors is commutative. Therefore, it is important to note that if the addition of the vector is done in any order then, the resultant of the addition of two vectors is the same.