Question

Assume that two liquids in a U-shape tube are water and oil. Compute the density of oil if water stands \[19cm\] above the interface and oil stands $24cm$ above the interface.

Answer 1

Hint: Pressure of a fluid at any point will be the same throughout its volume if we neglect its weight. But the weight of a fluid is not negligible so it varies according to depth of a point. The more is the depth, the more will be the pressure at that layer of fluid. The pressure at the same level of the liquid is constant at any point on that level irrespective of the shape of the container.

Formula used:
$P = {P_0} + h\rho g$
Where, $P$ is the pressure at depth $h$ of the fluid
${P_0}$ is the pressure at the surface of the fluid (atmospheric pressure)
$h$ is the depth of the liquid
$\rho $ is the density of the liquid
$g$ is acceleration due to gravity

Complete step by step answer:
Let’s consider a point $A$ at a depth of $h$ from the surface of the fluid. The pressure exerted at any point of the same depth is represented by the formula
$P = {P_0} + h\rho g$
We are given the question that, water stands $19cm$ above the interface and oil stands $24cm$ above the interface.
Let’s look at the following diagram.

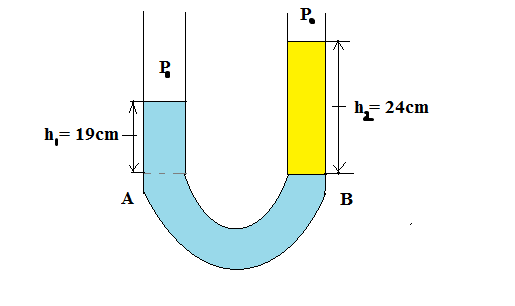
From the above figure, as points A and B are on the same level, pressure is the same at both the points.
Thus we can write, ${P_A} = {P_B}$ ……………………. (1)
Where, ${P_A}$ is the pressure at point A and ${P_B}$ is the pressure at point B.
Point A is at a depth ${h_1} = 19cm$ from the surface and point B is at a depth of ${h_2} = 24cm$ from the surface.
Let’s consider the densities of water and oil as ${\rho _1}$ and ${\rho _2}$ respectively.
Now substituting the corresponding values of variables in the pressure-depth formula, we get,
For water, at point A,
${P_A} = {P_0} + {h_1}{\rho _1}g$ ………. (2)
For oil, at point B,
${P_B} = {P_0} + {h_1}{\rho _1}g$ ………. (3)
From equation (1),
${P_A} = {P_B}$
Putting the values of ${P_A}$ and ${P_B}$ in this equation we get,
$ \Rightarrow {P_0} + {h_1}{\rho _1}g = {P_0} + {h_2}{\rho _2}g$
Cancelling ${P_0}$ from both sides, we get,
$ \Rightarrow {h_1}{\rho _1}g = {h_2}{\rho _2}g$
Dividing by $g$ in both sides we get,
$ \Rightarrow {h_1}{\rho _1} = {h_2}{\rho _2}$ ……….. (4)
The density of water in C.G.S units is $1gc{m^{ - 3}}$
Now substituting the values of ${h_1}$, ${\rho _1}$ and ${h_2}$ in equation (4), we get,
$ \Rightarrow 19 \times 1 = 24 \times {\rho _2}$
$ \Rightarrow {\rho _2} = \dfrac{{19}}{{24}} = 0.791gc{m^{ - 3}}$

Thus the density of oil in C.G.S units is $0.791gc{m^{ - 3}}$.

Notes: Water is taken as a universal measure of relative density of a fluid. The density of water at $4^\circ C$ is $1gc{m^{ - 3}}$ in C.G.S units and $1000kg{m^{ - 3}}$ in S.I units. Interface means the level where the fluids meet, which in this case is point B. the formula used is the pressure-depth formula because pressure is not constant throughout the fluid, but it is different at different depths.