
At the first minimum adjacent to the central maximum of a single-slit diffraction pattern the phase difference between the Huygens wavelet from the edge of the slit and the wavelet from the mid-point of the slit is
\[\left( a \right)\]$\dfrac{\pi }{8}radian$
\[\left( b \right)\]$\dfrac{\pi }{4}radian$
\[\left( c \right)\]$\dfrac{\pi }{2}radian$
\[\left( d \right)\]$\pi {\text{ }}radian$
Answer
217.8k+ views
Hint: When we see in single slit diffraction, a line perpendicular to the slit gets superadded. But when we see in double-slit diffraction, the light gets refracted once passing through the slits, to produce an interference pattern on the screen then the light waves commenced from those slits interfere with each other.
Complete step by step Solution:
Suppose there is the screen and there is a single slit placed in front of it. Then there is the distribution of energy on the outlets of the screen. The pattern formed will be in symmetric nature about its axis. Now we have to find the phase difference which should be between the edge of the slit and the wavelet which will be at the midpoint of the slit.
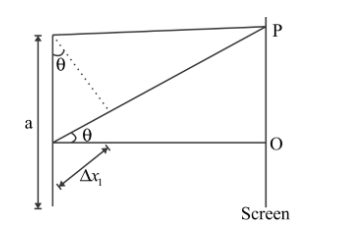
As we already know,
For the first minima at the position P
$ \Rightarrow a\sin \theta = \lambda $
Where $a$will be the length of the slit and $\lambda $will be its wavelength.
So now, phase difference will be calculated and it will be like this
$ \Rightarrow \vartriangle {\lambda _1} = \dfrac{{\vartriangle {x_1}}}{\lambda } \times 2\pi $
As we can see from the figure
$ \Rightarrow \vartriangle {x_1} = \left( {a/2} \right)\sin \theta $
And for first minima in the single-slit diffraction pattern,
$ \Rightarrow a\sin \theta = \lambda $
\[ \Rightarrow \dfrac{a}{2}\sin \theta = \dfrac{\lambda }{2}\]
Now we will put the above value in the $\vartriangle \phi $
$ \Rightarrow \dfrac{{\left( {a/2} \right)\sin \theta }}{\lambda } \times 2\pi $
After solving the above equation, we get
$ \Rightarrow \vartriangle {\phi _1} = \dfrac{\lambda }{{2\lambda }} \times 2\pi $
$ \therefore \pi {\text{ }}radian$
Hence, the option $d$ is the right choice for this question.
Note: Well, single slit diffraction involves sending a beam of light or electrons or alternative objects through one slit, whereas double-slit diffraction involves two slits. With one slim (comparable to the wavelength of the beam) slit, the beam diffracts broadly speaking altogether directions behind the slit and spreads everywhere a downstream viewing screen. With two slim slits, the beams from each slit additionally part generally; however currently the two beams overlap, making an interference pattern at the viewing screen.
Complete step by step Solution:
Suppose there is the screen and there is a single slit placed in front of it. Then there is the distribution of energy on the outlets of the screen. The pattern formed will be in symmetric nature about its axis. Now we have to find the phase difference which should be between the edge of the slit and the wavelet which will be at the midpoint of the slit.

As we already know,
For the first minima at the position P
$ \Rightarrow a\sin \theta = \lambda $
Where $a$will be the length of the slit and $\lambda $will be its wavelength.
So now, phase difference will be calculated and it will be like this
$ \Rightarrow \vartriangle {\lambda _1} = \dfrac{{\vartriangle {x_1}}}{\lambda } \times 2\pi $
As we can see from the figure
$ \Rightarrow \vartriangle {x_1} = \left( {a/2} \right)\sin \theta $
And for first minima in the single-slit diffraction pattern,
$ \Rightarrow a\sin \theta = \lambda $
\[ \Rightarrow \dfrac{a}{2}\sin \theta = \dfrac{\lambda }{2}\]
Now we will put the above value in the $\vartriangle \phi $
$ \Rightarrow \dfrac{{\left( {a/2} \right)\sin \theta }}{\lambda } \times 2\pi $
After solving the above equation, we get
$ \Rightarrow \vartriangle {\phi _1} = \dfrac{\lambda }{{2\lambda }} \times 2\pi $
$ \therefore \pi {\text{ }}radian$
Hence, the option $d$ is the right choice for this question.
Note: Well, single slit diffraction involves sending a beam of light or electrons or alternative objects through one slit, whereas double-slit diffraction involves two slits. With one slim (comparable to the wavelength of the beam) slit, the beam diffracts broadly speaking altogether directions behind the slit and spreads everywhere a downstream viewing screen. With two slim slits, the beams from each slit additionally part generally; however currently the two beams overlap, making an interference pattern at the viewing screen.
Recently Updated Pages
Addition of Three Vectors: Methods & Examples

Addition of Vectors: Simple Guide for Students

Algebra Made Easy: Step-by-Step Guide for Students

Relations and Functions: Complete Guide for Students

Analytical Method of Vector Addition Explained Simply

Arithmetic, Geometric & Harmonic Progressions Explained

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26

NCERT Solutions For Class 11 Physics Chapter 8 Mechanical Properties Of Solids

Motion in a Straight Line Class 11 Physics Chapter 2 CBSE Notes - 2025-26

NCERT Solutions for Class 11 Physics Chapter 7 Gravitation 2025-26

Understanding Atomic Structure for Beginners




