Question

Dependence of intensity of gravitational field ($E$) of earth with distance ($r$) from centre of earth is correctly represented by
(A)

(B)

(C)

(D)

Answer 1

Hint: The intensity of the gravitational field at the centre is zero and for a point inside the earth, intensity is proportional to the inverse of the distance from the centre. For a point outside the surface of the earth, intensity is inversely proportional to the square of the distance from the centre including the radius.

Formula Used: The formulae used in the solution are given here.
The force of gravitational attraction exerted on the test particle is given by- ${F_g} = \dfrac{{GMm}}{{{r^2}}}\hat r$ where the $O\vec R = r$, $G$ is the universal gravitational constant, $R$ is the radius of the Earth and $M$ is the mass of the Earth.
$\vec E = \dfrac{{{{\vec F}_g}}}{m}$ where the mass of the particle is $m$.

Complete Step by Step Solution: The space around a body where the gravitational force exerted by it can be experienced by any other particle is known as the gravitational field of the body. The strength of this gravitational field is referred to as intensity, and it varies from point to point.
Consider the gravitational field of a particle of mass m located at the origin (O).
The force of gravitational attraction exerted on the test particle is given by- ${F_g} = \dfrac{{GMm}}{{{r^2}}}\hat r$ where the $O\vec R = r$
The strength of the gravitational field is known as gravitational field intensity. It is the gravitational force acting on a unit test mass.
$\vec E = \dfrac{{{{\vec F}_g}}}{m}$ where the mass of the particle is $m$.
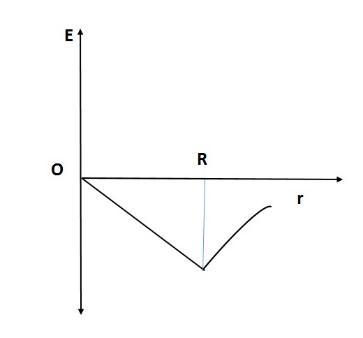
Intensity of gravitational field ($E$) of the earth with distance ($r$) from the centre of the earth:
${E_{inside}} = - \dfrac{{GMr}}{{{R^3}}}$ where $G$ is the universal gravitational constant, $R$ is the radius of the Earth and $M$ is the mass of the Earth.
Hence, we can write, ${E_{inside}} \propto - r$.
${E_{outside}} = - \dfrac{{GM}}{{{r^2}}}$
$ \Rightarrow {E_{outside}} \propto - \dfrac{1}{{{r^2}}}$
From the above given equations, we derive the relations between the distance ($r$) from centre of earth and the intensity of gravitational field ($E$) of earth:
${E_{outside}} \propto - \dfrac{1}{{{r^2}}}$ and ${E_{inside}} \propto - r$.
The graph shall look like:


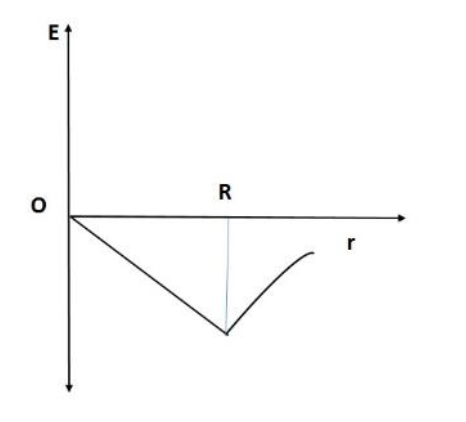
Hence, the correct answer is Option A.

Note: Gravity or Gravitation is a phenomenon in which all things with energy or mass, including galaxy, stars, planets, and lights, are attracted. Gravity gives weight to the mass on earth. The gravitational attraction of the gaseous matter present in the universe caused it to begin coalescing and form stars and group these stars into a galaxy. Because of gravity only, many large scale structures are present in the universe. Gravity range is unlimited but as objects get further away its effects become increasingly weaker. Out of the four fundamental forces, gravity is said to be the weakest force. It has no significant influence at the level of the subatomic particles. At the microscopic scale, it is known as the dominant interaction, and it is the cause of the formation of shape and trajectory of astronomical bodies. In the universes, the earliest trace of gravity was possibly in quantum gravity, super gravity, and ordinary time and space, possibly from the primitive state.