Question

Determine the time spent by a particle in a magnetic field and change in its momentum.

Answer 1

Hint To find the time spent by a particle in a magnetic field we find the length of the arc (path taken by the particle in the magnetic field) by multiplying the angle made by the arc with the radius of the arc. Substituting the equation of radius in the equation of length of arc and dividing it by velocity of the particle, we get the time spent by the particle.
The change in momentum is the difference in momentum of the particle before entering the magnetic field and while leaving the magnetic field. The change in momentum is also called the impulse.
Formula used
Time spent by the particle is $t = \dfrac{l}{v}$
Change in momentum or impulse is $\Delta p = \Delta mv$
Here, Length of the arc is represented , Velocity of the particle is represented by , Time spent by the particle is given by , and Change in momentum is given by

Complete Step by step solution
The given diagram explains the path taken by the particle


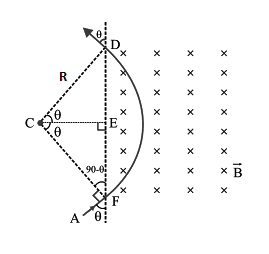
Length of the arc (path taken by particle)
$ \Rightarrow l = 2\theta R$
Angle made by arc $\theta + \theta = 2\theta $
Substituting the value of radius in the length of the arc,
$ \Rightarrow R = \dfrac{{mv}}{{qB}} $
$ \Rightarrow l = \dfrac{{2\theta mv}}{{qB}} $

Here, $m,v,q,B$ represent the mass, velocity, charge of the particle, and the magnitude of the magnetic field into the plane respectively.
Dividing the length of the arc with the velocity we get the time spent by a particle in the magnetic field
$ \Rightarrow t = \dfrac{l}{v} $
$ \Rightarrow t = \dfrac{{2\theta m}}{{qB}} $
Time spent is $t = \dfrac{{2\theta m}}{{qB}}$

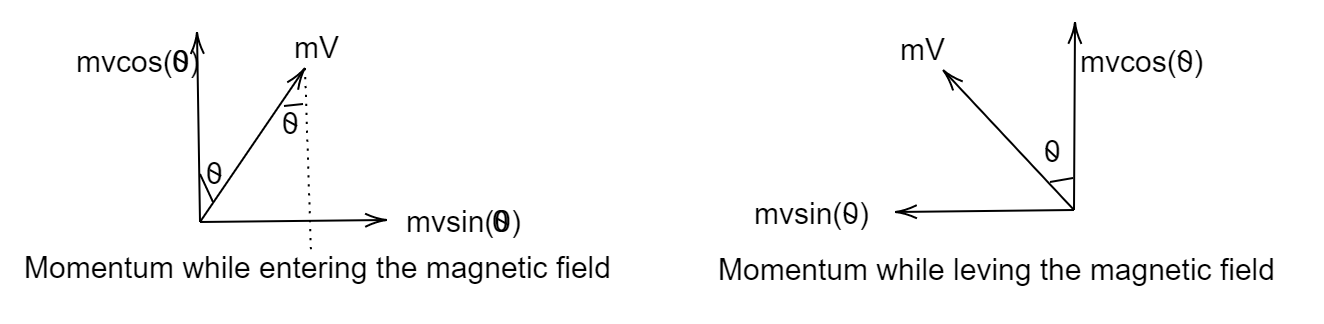
Momentum while entering the magnetic field is ${p_e} = mvcos\theta j + mv\sin \theta i$
Momentum while leaving the magnetic field is ${p_l} = mvcos\theta j - mv\sin \theta i$
The difference of these momentum gives us the change in momentum,
$ \Rightarrow {p_l} - {p_e} = \Delta p $
$ \Rightarrow \Delta p = (mvcos\theta j - mv\sin \theta i) - (mvcos\theta j + mv\sin \theta i) $
$ \Rightarrow \Delta p = - 2mv\sin \theta i $

The change in momentum is $\Delta p = - 2mv\sin \theta i$

Note Students may get confused with the angle with which the particle enters the magnetic field. Students may presume it as$90^\circ $. We should take the angle as $\theta $ and proceed. Time spent can also be found by dividing the angle made by an arc with angular velocity.