
Find the current in wire AB
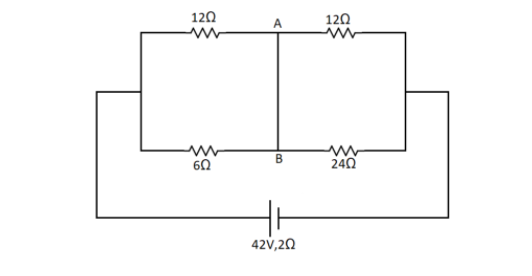
Answer
141.9k+ views
Hint: The wire AB in between connects all the 4 resistances. So by drawing the circuit in a simpler way, we can find the equivalent resistance. Then we can calculate the current being drawn from the cell using the emf of the call. This will be the current in the wire AB.
Formula Used In this solution, we are going to use the following formula,
And
Complete Step by Step Solution
To find the current in the wire AB we need to first redraw the circuit in a more simple way. Here the points A and B are the same point joined by a wire. So we can draw the circuit as,
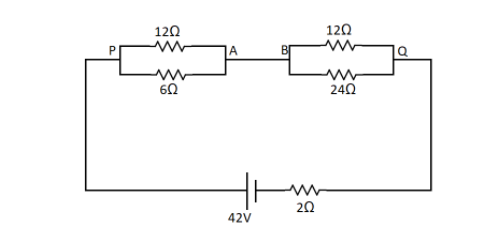
From this circuit we can see that there are 2 parallel circuits consisting of 2 resistances each.
Let us first find the equivalent resistance between the points P and Q. The formula for parallel combination is
Here we have
So substituting we get,
Taking LCM as 12
So by taking the reciprocal we get,
Similarly, between the points B and Q we have 2 resistances in parallel combination. So again here
Substituting we get,
Taking LCM as 24,
Taking the reciprocal we get,
Now the resistance
Here
So we get,
Therefore, we get the equivalent resistance as,
Now it is given that the battery has an emf of
So from the Ohm’s law
Substituting we get,
This is the whole current that is in the flowing through the wire. Now since between the points A and B the current doesn’t get divided, so the current in the wire AB will be
Note: In the given circuit, when the two resistances are in series condition then the current that flows in them both is the same whereas when the resistances are in parallel, the potential difference is the same across the resistances but the current varies. So the current in the 2 wires between P and A are different and depends on the magnitude of the resistance.
Formula Used In this solution, we are going to use the following formula,
And
Complete Step by Step Solution
To find the current in the wire AB we need to first redraw the circuit in a more simple way. Here the points A and B are the same point joined by a wire. So we can draw the circuit as,

From this circuit we can see that there are 2 parallel circuits consisting of 2 resistances each.
Let us first find the equivalent resistance between the points P and Q. The formula for parallel combination is
Here we have
So substituting we get,
Taking LCM as 12
So by taking the reciprocal we get,
Similarly, between the points B and Q we have 2 resistances in parallel combination. So again here
Substituting we get,
Taking LCM as 24,
Taking the reciprocal we get,
Now the resistance
Here
So we get,
Therefore, we get the equivalent resistance as,
Now it is given that the battery has an emf of
So from the Ohm’s law
Substituting we get,
This is the whole current that is in the flowing through the wire. Now since between the points A and B the current doesn’t get divided, so the current in the wire AB will be
Note: In the given circuit, when the two resistances are in series condition then the current that flows in them both is the same whereas when the resistances are in parallel, the potential difference is the same across the resistances but the current varies. So the current in the 2 wires between P and A are different and depends on the magnitude of the resistance.
Recently Updated Pages
Uniform Acceleration - Definition, Equation, Examples, and FAQs

Difference Between Mass and Weight

Difference Between Circuit Switching and Packet Switching

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

JEE Advanced Weightage 2025 Chapter-Wise for Physics, Maths and Chemistry




