Question

Find the second excitation energy of $L{i^{2 + }}$ .
(A) 108.8 $eV$
(B) 81.6 $eV$
(C) 13.6 $eV$
(D) 95.2 $eV$

Answer 1

Hint: To solve this question one needs to know the atomic number of different elements. Also, by second excitation we mean that the electron is jumping from ${1^{st}}$ to ${3^{rd}}$ energy level. To find the second excitation energy of an element we subtract the energy of ${1^{st}}$ energy level from the energy of ${3^{rd}}$ energy level.

Complete Step by Step Solution:
It is given that an electron jumps from ${1^{st}}$ energy level to the ${3^{rd}}$ energy level i.e., second excited state.


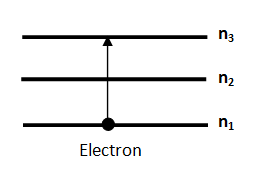
We know that energy of ${n^{th}}$ energy level of an element is $ - \dfrac{{13.6 \times {Z^2}}}{{{n^2}}}$ where Z is the atomic number of the element and n is the energy level of the electron. This energy is in electron volts $(eV)$ . Atomic number is the number of protons in the nucleus of an atom.

Now to find the second excitation energy $\left( E \right)$ of $L{i^{2 + }}$ we subtract the energy of ${1^{st}}$ energy level \[\left( {{E_1}} \right)\] from the energy of ${3^{rd}}$ energy level $\left( {{E_3}} \right)$ .
Therefore, $E = {E_3} - {E_1}$
 \[E = - \dfrac{{13.6 \times {Z^2}}}{{{n_3}^2}} - \left( { - \dfrac{{13.6 \times {Z^2}}}{{{n_1}^2}}} \right)\] ...(1)
Now we know that the atomic number of $Li$ is 3, so here we get $Z = 3$ .
Also, ${n_{_3}}$ is the ${3^{rd}}$ energy level and ${n_1}$ is the ${1^{st}}$ energy level, so we get that ${n_{_3}} = 3$ and ${n_1} = 1$ .
Thus, equation (1) becomes,
\[E = - \dfrac{{13.6 \times {3^2}}}{{{3^2}}} - \left( { - \dfrac{{13.6 \times {3^2}}}{{{1^2}}}} \right)\]
\[E = - \dfrac{{13.6 \times {3^2}}}{{{3^2}}} + \dfrac{{13.6 \times {3^2}}}{{{1^2}}}\]
Taking $13.6 \times {3^2}$ common from both the terms we get,
 $E = - 13.6 \times {3^2} \times \left( {\dfrac{1}{{{3^2}}} - \dfrac{1}{{{1^2}}}} \right)$
 $E = - 13.6 \times 9 \times \left( {\dfrac{1}{9} - \dfrac{1}{1}} \right)$

Solving the brackets,
 $E = - 13.6 \times 9 \times \left( {\dfrac{{1 - 9}}{9}} \right)$
 $E = - 13.6 \times 9 \times \left( {\dfrac{{ - 8}}{9}} \right)$

Multiplying all the terms, we get
 $E = - 13.6 \times \left( { - 8} \right)$
Thus, $E = 108.8\,eV$
Hence, the correct option is A.

Note: First thing to keep in mind in all such questions is that second excited state is not the ${2^{nd}}$ energy level of the element, it is the ${3^{rd}}$ energy level. Thus, we can say that the ${n^{th}}$ excited state is ${(n + 1)^{th}}$ energy level of any element. Also, the energy obtained by this method is in electron volts $(eV)$ and not in Joule $\left( J \right)$ . To convert $eV$ into $J$ use the conversion equation: $1eV = 1.602 \times {10^{ - 19}}J$ .