Question

If a simple pendulum has a significant amplitude (up to a factor of $\dfrac{1}{e}$ of original) only in the period between $t = 0s$ to $t = \tau s$, then $\tau $ may be called as the average life of the pendulum. When the spherical bob of the pendulum suffers a retardation (due to viscous drag) proportional to its velocity, with $b$ as the constant of proportionality, the average time of the pendulum is (assuming the damping is small):

Answer 1

Hint: To solve the given problem we can use the concept of motion; we can write the equation motion and if we differentiate the motion equation, we can get the answer.

Formula used:
The equation of motion:
$ \Rightarrow F = - kx - bv$
Where $v$ is the velocity.

Complete step by step answer:
We can try to solve the given problem.
Consider the equation of the motion for the simple pendulum suffering retardation, that is,
$ \Rightarrow F = - kx - bv$
We can use the second-order differential equation is,
$ \Rightarrow m\dfrac{{{d^2}x}}{{d{t^2}}} + kx + b\dfrac{{dk}}{{dt}} = 0$
We can divide and multiply the term m. we get,
$ \Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + \dfrac{k}{m}x + \dfrac{b}{m}\dfrac{{dx}}{{dt}} = 0$
Rearrange the terms according to the degrees of x. we get.
\[ \Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} + \dfrac{b}{m}\dfrac{{dx}}{{dt}} + \dfrac{k}{m}x = 0\]..........1
When we solve equation 1, we get the solution as $x = {e^{\lambda t}}$. We can differentiate this equation as,
$ \Rightarrow \dfrac{{dx}}{{dt}} = \lambda {e^{\lambda t}}$
If we differentiate this again, we get,
$ \Rightarrow \dfrac{{{d^2}x}}{{d{t^2}}} = {\lambda ^2}{e^{\lambda t}}$
We can substitute the values in equation 1 we get,
\[ \Rightarrow {\lambda ^2}{e^{\lambda t}} + \dfrac{b}{m}\lambda {e^{\lambda t}} + \dfrac{k}{m}{e^{\lambda t}} = 0\]
We can divide and multiply ${e^{\lambda t}}$we get,
\[ \Rightarrow {\lambda ^2} + \dfrac{b}{m}\lambda + \dfrac{k}{m} = 0\]
The value for finding the $\lambda $is,
$ \Rightarrow \lambda = \dfrac{{\dfrac{{ - b}}{m} \pm \sqrt {\dfrac{{{b^2}}}{{{m^2}}} - 4\dfrac{k}{m}} }}{2}$
We can divide and multiply the term m, we get,
$ \Rightarrow \lambda = \dfrac{{ - b \pm \sqrt {{b^2} - 4km} }}{{2m}}$
We can solve the equation 1 for $x$, we get,
$ \Rightarrow x = {e^{\dfrac{{ - b}}{{2m}}t}}$
On solving the equation, we get,
$ \Rightarrow A\cos \left( {\omega _0^2 - {\lambda ^2}} \right)$
From this, we have the value for omega. That is,
$ \Rightarrow \omega = \sqrt {\omega _0^2 - {\lambda ^2}} $
Where ${\omega _0} = \dfrac{k}{m}$and $\lambda = \dfrac{b}{2}$
Therefore, the average life is given as
$ \Rightarrow \dfrac{1}{\lambda } = \dfrac{2}{b}$
Hence the average time of the pendulum is $\dfrac{2}{b}$.
This is the free body diagram that represents the simple pendulum values along with the directions.

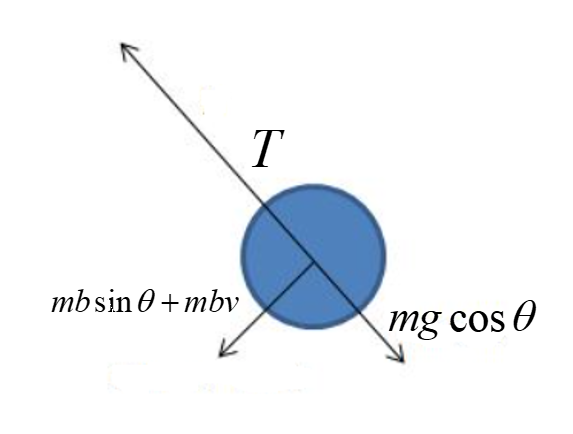
Additional information:
When a point mass is attached to the light inextensible string and it is suspended from the fixed support is known as a simple pendulum. The Mean position is determined by the vertical line from the fixed support.

Note: There are some assumptions for calculating the time period. They are, there will be a negligible distance between the system and the air, the pendulum arm is not compressible, the swings of the pendulum are the perfect plane and the gravity remains always constant.