Question

If from the vertex of a parabola, a pair of chords be drawn at right angles to one another and with these chords as adjacent sides a rectangle be made, prove that the locus of the further angle of the rectangle is the parabola \[{{y}^{2}}=4a\left( x-8a \right)\].

Answer 1

Hint: The mid-points of the diagonals of a rectangle are the same .
 Let’s take the equation of parabola as \[{{y}^{2}}=4ax\].

We know the vertex of this parabola is at \[V\left( 0,0 \right)\].
Let \[A\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[B\left( at_{2}^{2},2a{{t}_{2}} \right)\] be the two vertices of the rectangle.


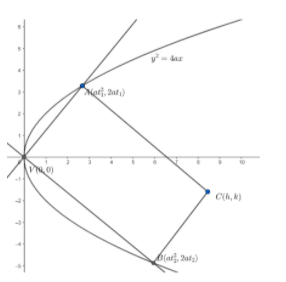
Now, we are given that the two chords are perpendicular.
We know that if two lines are perpendicular to each other , then the product of their slopes is equal to \[-1\].
So, slope of \[VA\times \] slope of \[VB=-1\]
Now , we will find the slope of \[VA\] and slope of \[VB\].
We know , the slope of the line joining two points \[({{x}_{1}},{{y}_{1}})\] and \[({{x}_{2}},{{y}_{2}})\] is given as \[m=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}\].
So , slope of \[VA=\dfrac{2a{{t}_{1}}-0}{at_{1}^{2}-0}=\dfrac{2}{{{t}_{1}}}\]
And , slope of \[\text{ }VB=\dfrac{2a{{t}_{2}}-0}{at_{2}^{2}-0}=\dfrac{2}{{{t}_{2}}}\]
So, \[\dfrac{2}{{{t}_{1}}}\times \dfrac{2}{{{t}_{2}}}=-1\]
\[\Rightarrow {{t}_{1}}{{t}_{2}}=-4....\left( i \right)\]
We need to find the locus of further vertex.
So , we will consider the further vertex to be \[C\left( h,k \right)\].
Now , in the question it is given that \[AVBC\] is a rectangle.
We know the diagonals of a rectangle bisect each other.
So , midpoint of \[AB=\] midpoint of \[\text{ }VC.....(ii)\]
Now, we will find the midpoints of \[AB\] and \[VC\].
Midpoint of
\[\text{ }AB=\left( \dfrac{at_{1}^{2}+at_{2}^{2}}{2},\dfrac{2a{{t}_{1}}+2a{{t}_{2}}}{2} \right)\]
\[=\left( \dfrac{at_{1}^{2}+at_{2}^{2}}{2},a{{t}_{1}}+a{{t}_{2}} \right)....\left( iii \right)\]
Midpoint of \[\text{ VC}=\left( \dfrac{h+0}{2},\dfrac{k+0}{2} \right)\]
\[=\left( \dfrac{h}{2},\dfrac{k}{2} \right).....\left( iv \right)\]
From \[\left( ii \right),\left( iii \right)\]and \[\left( iv \right)\], we can say
\[\dfrac{h}{2}=\dfrac{at_{1}^{2}+at_{2}^{2}}{2}\] and \[\dfrac{k}{2}=a{{t}_{1}}+a{{t}_{2}}\]
Now, \[\dfrac{h}{2}=\dfrac{at_{1}^{2}+at_{2}^{2}}{2}\]
\[\Rightarrow t_{1}^{2}+t_{2}^{2}=\dfrac{h}{a}....\left( v \right)\]
and \[\dfrac{k}{2}=\left( a{{t}_{1}}+a{{t}_{2}} \right)\]
\[\Rightarrow {{t}_{1}}+{{t}_{2}}=\dfrac{k}{2a}.....\left( vi \right)\]
Squaring both sides we get
\[t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}}=\dfrac{{{k}^{2}}}{4{{a}^{2}}}.....\left( vii \right)\]
From equation \[\left( i \right),\left( v \right)\]and \[\left( vii \right)\]
\[\dfrac{h}{a}-8=\dfrac{{{k}^{2}}}{4{{a}^{2}}}\]
or \[{{k}^{2}}=4a\left( h-8a \right)\]…….equation\[(viii)\]
Now, to find the locus of \[C\left( h,k \right)\], we will substitute \[(x,y)\] in place of \[\left( h,k \right)\] in equation \[(viii)\]
So, the locus of \[C\left( h,k \right)\] is given as \[{{y}^{2}}=4a\left( x-8a \right)\]

Note: While simplifying the equations , please make sure that sign mistakes do not occur. These mistakes are very common and can cause confusions while solving. Ultimately the answer becomes wrong. So, sign conventions should be carefully taken .