Question

If ${K_i}$ and ${K_p}$ are the effective spring constant in series and parallel combination of springs as shown in figure, find \[\dfrac{{{K_i}}}{{{K_p}}}\].

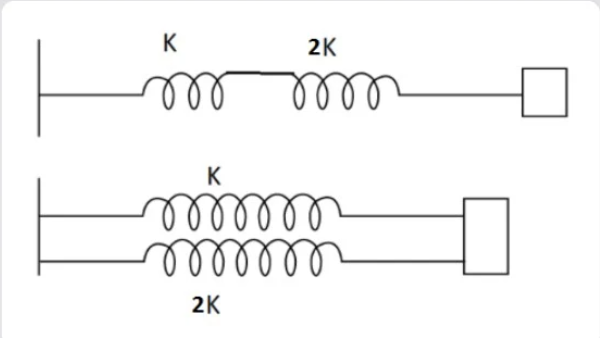
A. 9/2
B. 3/7
C. 2/9
D. 7/3

Answer 1

Hint: Try to recall the concept of dividing current in branches having resistance \[{R_1}\] and \[{R_2}\] which are firstly connected in series and secondly in parallel. From that concept we will get the idea of adding spring constants, either springs are connected in series or connected in parallel. And then simply take the ratio of and we will get the answer.

Complete step by step answer:
First we will see the concept of adding spring constants when they are connected in
1. Series
2. Parallel

Case:1 When Springs are connected in series.
When two spring are connected in series having spring constants \[{K_1}\] and \[{K_2}\] as shown in below figure

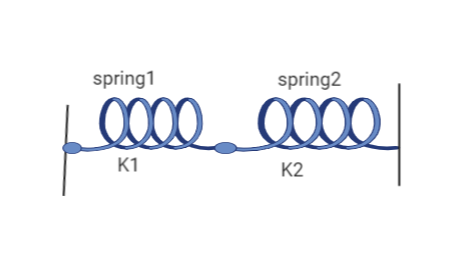
Then the resulting Spring constant ${K_r}$ is given by the formula:
\[\dfrac{1}{{{K_{}}}} = \dfrac{1}{{{K_1}}} + \dfrac{1}{{{K_2}}}\]
Now from the question
\[{K_1} = K\]
\[{K_2} = 2K\]
Putting values in formula
\[\dfrac{1}{{{K_r}}} = \dfrac{1}{K} + \dfrac{1}{{2K}}\]
\[\dfrac{1}{{{K_r}}} = \dfrac{{2K + K}}{{2{K^2}}}\]
\[\dfrac{1}{{{K_r}}} = \dfrac{3}{{2K}}\]
\[{K_r} = \dfrac{{2K}}{3}\]

Case 2: When springs are connected in parallel
When two spring are connected in parallel having spring constants \[{K_1}\] and \[{K_2}\] as shown in below figure

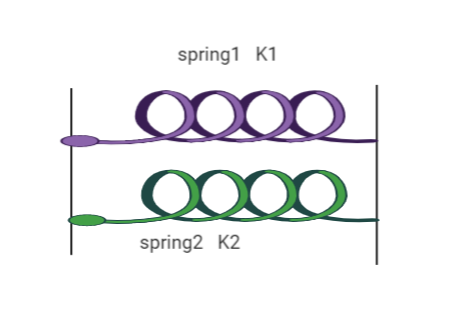
Then the resulting Spring constant \[{K_p}\] is given by the formula:
\[{K_p} = {K_1} + {K_2}\]
Given values of \[{K_1}\] and \[{K_2}\]from question:
\[{K_1} = K\]
\[{K_2} = 2K\]
Putting values in above equation:
\[{K_p} = K + 2K\]
\[{K_p} = 3K\]
Now we have both spring constant
\[\dfrac{{{K_i}}}{{{K_p}}} = \dfrac{{{K_r}}}{{{K_p}}} = \dfrac{{\dfrac{{2K}}{3}}}{{3K}}\]
\[\dfrac{{{K_i}}}{{{K_p}}} = \dfrac{2}{9}\]
Hence, option C is correct.

Note: This concept can be used to combine two springs and replace it with a new one. Not only we are bound to combine two springs we can also combine many strings. If the spring constant of a spring is high then it is difficult to stretch it more while spring having less or low spring constant can be elongated much more than the previous one.