Question

If the resultant vector of $\overrightarrow{A}$ and $\overrightarrow{B}$ makes an angle $\alpha$ with $\overrightarrow{A}$ and $\beta$ with $\overrightarrow{B}$ , then:
A) $\alpha <\beta$
B) $\alpha <\beta$ if $A<B$
C) $\alpha <\beta$ if $A>B$
D) $\alpha <\beta$ if $A=B$

Answer 1

Hint: Always the resultant vector incline towards the vector which is higher in magnitude. If the two vectors have the same magnitude, the resultant vector will make equal angles with the both two vectors.

Complete step by step solution:
Let’s solve this problem with the help of a diagram. Two vectors $\overrightarrow{A}$ and $\overrightarrow{B}$ are drawn and the resultant is a vector $\overrightarrow{R}$ . The resultant vector $\overrightarrow{R}$ makes an angle $\alpha$ with the vector $\overrightarrow{A}$ and the resultant vector $\overrightarrow{R}$ makes an angle $\beta$ with the vector $\overrightarrow{B}$

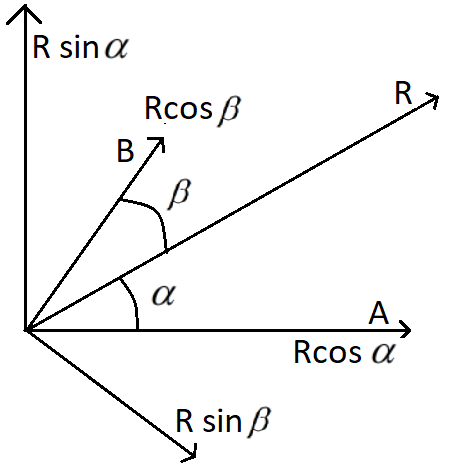
From the details given in the diagram we can see that
Angle between the vector $\overrightarrow{A}$ and the resultant vector $\overrightarrow{R}$ = $\alpha$ .
Angle between the vector $\overrightarrow{B}$ and the resultant vector $\overrightarrow{R}$ = $\beta$ .
Total angle between the vector $\overrightarrow{A}$ and vector $\overrightarrow{B}$ = $\alpha +\beta$ .
From the diagram it is known that,
$A=R\cos \alpha$
$B=R\cos \beta$
Let’s discuss the three cases :
When $\overrightarrow{A}$ = $\overrightarrow{B}$
Applying the values of vector $\overrightarrow{A}$ and vector $\overrightarrow{B}$ ,
$\overrightarrow{A}$ = $\overrightarrow{B}$
$\Rightarrow R\cos \alpha =R\cos \beta$
Cancelling equal terms on the right hand side and left hand side of the above equation we get:
$\cos \alpha =\cos \beta$
$\Rightarrow \alpha =\beta$
When $\overrightarrow{A}$<$\overrightarrow{B}$
Applying the values of vector $\overrightarrow{A}$ and vector $\overrightarrow{B}$ ,
$\overrightarrow{A}$<$\overrightarrow{B}$
 $$\Rightarrow R\cos \alpha <R\cos \beta$$
Cancelling equal terms on the right hand side and left hand side of the above equation we get:
$\cos \alpha <\cos \beta$
$\Rightarrow \alpha >\beta$
When $\overrightarrow{A}$>$\overrightarrow{B}$
Applying the values of vector $\overrightarrow{A}$ and vector $\overrightarrow{B}$ ,
$\overrightarrow{A}$>$\overrightarrow{B}$
$$\Rightarrow R\cos \alpha >R\cos \beta$$
Cancelling equal terms on the right hand side and left hand side of the above equation we get:
$\cos \alpha >\cos \beta$
$\Rightarrow \alpha <\beta$

By analysing these three cases we get the angle between the resultant vector $\overrightarrow{R}$ and the vector $\overrightarrow{A}$ , $\alpha$ is less than angle between the resultant vector $\overrightarrow{R}$ and the vector $\overrightarrow{B}$ , $\beta$
That is, $\alpha <\beta$ when $A>B$

Final answer is option (C): $\alpha <\beta$ if $A>B$.

Note: If two vectors acting simultaneously at a point can be represented both in magnitude and direction by the adjacent sides of a parallelogram drawn from a point, then the resultant vector is represented both in magnitude and direction by the diagonal of the parallelogram passing through that point.