Question

In a school, there are $3$ types of games to be played. Some of the students play $2$ types of games, but none play all $3$ games. Which Venn diagrams can justify the above statements?

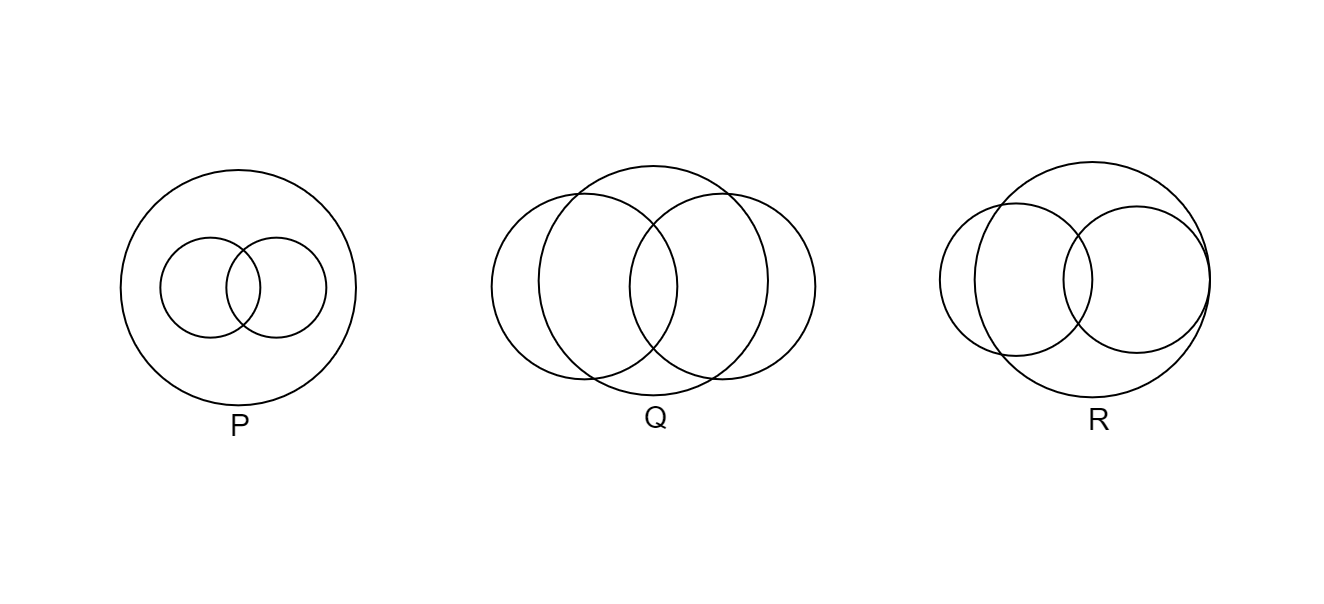
1. P and R
2. P and Q
3. None of these
4. Q and R

Answer 1

Hint: Here, we are given three Venn diagrams P, Q, and R. We have to select which of the diagram justifies the statement that some students play two games, but none plays all three games. It means, we have to check which of the diagram is not of intersection.

Formula Used:
Given Venn diagram are of intersection i.e., $A \cap B \cap C$

Complete step by step Solution:
Let, A, B, and C be the first, second, and third games that are played by the student in school
Now, let the condition be some students play two games, but none play all three games.
It means, in the Venn diagram there should be no common part in all three games.
There should be a common part in any of the two games,
Case 1: A and B
Case 2: B and C
Case 3: A and C
A Venn diagram of the given statement is attached below,
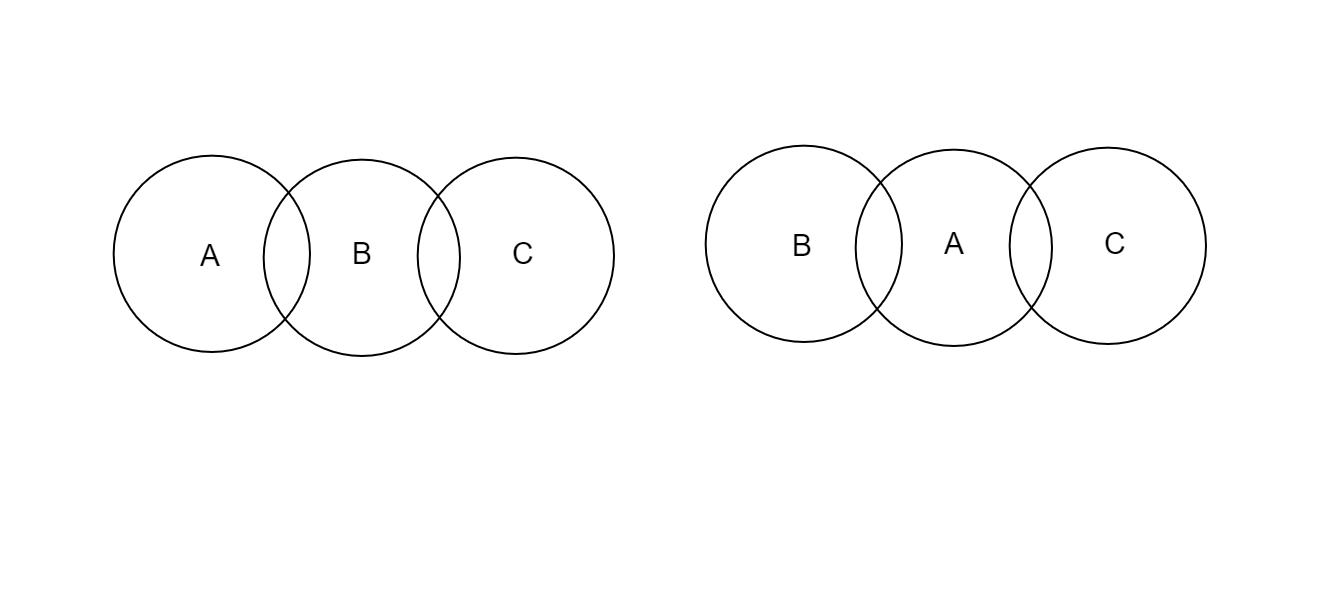Now, in the given Venn diagram P, Q, and R, there are common parts in all three games. This implies that there are some students who play all three games which contradicts the statement that none of the students plays all three games.

Hence, the correct option is 3.

Note: The key concept involved in solving this problem is a good knowledge of Union and Intersection. Students must know that the union of two sets P and Q corresponds to the set of elements that are included in set P, set Q, or both sets P and Q. The intersection of two subsets of the universal set U, A, and B, is the set that contains all of the elements that are shared by both A and B.