Question

In an n – sided regular polygon, the probability that the two diagonal chosen at random will intersect inside the polygon is:
(a) \[\dfrac{^{{{2}^{2}}}{{C}_{2}}}{^{\left( ^{n}{{C}_{1}}-n \right)}{{C}_{2}}}\]
(b) \[\dfrac{^{n\left( n-1 \right)}{{C}_{2}}}{^{\left( ^{n}{{C}_{2}}-n \right)}{{C}_{2}}}\]
(c) \[\dfrac{^{n}{{C}_{4}}}{^{\left( ^{n}{{C}_{2}}-n \right)}{{C}_{2}}}\]
(d) None of these

Answer 1

Hint: First of all find the number of diagonals of the polygon by selecting any two vertices out of n and subtracting from it the number of sides (n). Now, select two diagonals out of the total diagonals as it would be the number of total outcomes. Also, find the favorable outcomes by counting the number of the quadrilateral formed by the vertices of the n sided polygon because a quadrilateral has a unique set of diagonals intersecting inside it. Now, find the probability as \[\dfrac{\text{Favorable Outcomes}}{\text{Total Outcomes}}\].

Complete step-by-step answer:

In a regular n sided polygon, we have to find the probability of two diagonals chosen at random will intersect inside the polygon. Let us consider an n sided polygon

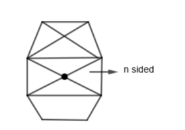
We know that n sided polygon is made up of n points or n vertices. By joining any two points out of these n points, we either get sides of the polygon or the diagonals of the polygon. So, we get,
(Number of ways joining 2 vertices out of n vertices of n sided polygon) = (Number of diagonals in n sided polygon) + (Number of sides of n sided polygon)
We know that the number of ways of selecting r out of n things Is given by \[^{n}{{C}_{r}}\] and the number of sides in the n sided polygon is n. By using these, we get,
\[^{n}{{C}_{2}}=\left( \text{No}\text{.of diagonals in n sided polygon} \right)+n\]
So, we get the number of diagonals in n sided polygon = \[^{n}{{C}_{2}}-n\]
Now, as we need to find the probability for the intersection of the two diagonals, we get the sample space or total number of outcomes as,
Selection of 2 diagonals out of \[^{n}{{C}_{2}}-n\] diagonals \[={{\text{ }}^{\left( ^{n}{{C}_{2}}-n \right)}}{{C}_{2}}.....\left( i \right)\]
Now, to find the total number of diagonal pairs that intersect inside the polygon, we only have to count the total number of quadrilaterals that can be formed from the vertices of n sided polygon. The reason for this is that a quadrilateral always has a unique pair of diagonal intersections inside it and so the number of quadrilaterals is the same as the number of pairs of the diagonals meeting inside the n sided polygon. So, we get,
Total number of the quadrilateral that can be formed by n vertices of n – sided polygon = \[^{n}{{C}_{\left( \text{vertices of quadrilateral} \right)}}\]
We know that the number of vertices in a quadrilateral is 4. So, we get,
Total number of quadrilaterals = \[^{n}{{C}_{4}}\]
So, we get favorable outcomes = \[^{n}{{C}_{4}}.....\left( ii \right)\]
We know that Probability of an event = \[\dfrac{\text{Favorable Outcomes}}{\text{Total Outcomes}}\]
By substituting the value of total outcomes and favorable outcomes from equation (i) and (ii) respectively, we get,
The probability that two diagonals are chosen will lie inside the n - sided polygon
\[=\dfrac{\left( ^{n}{{C}_{4}} \right)}{^{\left( ^{n}{{C}_{2}}-n \right)}{{C}_{2}}}\]
Hence, the option (c) is the right answer.

Note: In this question, students must note that this formula will work only for positive integers \[n\ge 4\], as we know that the sides of the polygon cannot be negative. For n = 3, that is for the triangle, this formula won’t make sense (the formula will give probability as \[\dfrac{-1}{3}\], which is absurd). For the triangle, the probability is 0 because it has only 3 vertices, so no quadrilateral or diagonals can be formed in it.