Question

In the circuit shown the current in the $1\Omega $resistor is:

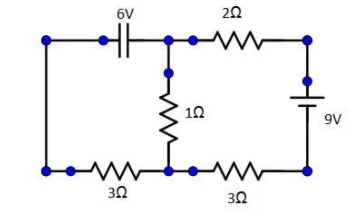
(A) 1.3A, from P to Q
(B) 0A
(C) 0.13A, from Q to P
(D) 0.13A, from P to Q

Answer 1

Hint: The question can be solved by grounding one end of the wire and then applying Kirchhoff’s Current Law to the loop formed. Kirchhoff’s Voltage Law can also be used to solve this problem.

Complete Step by Step Solution: Kirchhoff’s Current Law, deals with the conservation of charge entering and leaving a junction. Kirchhoff’s Current Law, often shortened to KCL, states that “The algebraic sum of all currents entering and exiting a node must equal zero.”
This law is used to describe how a charge enters and leaves a wire junction point or node on a wire.
Connect the lower wire of the $1\Omega $ resistor to the ground (Q end) and apply KCL. Consider the grounded circuit as shown below.

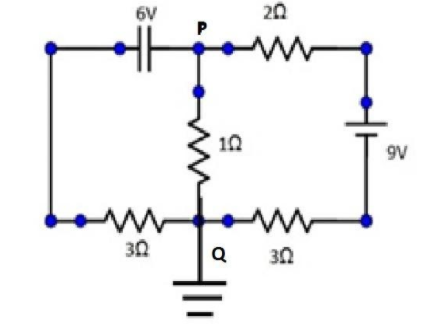
Applying, KCL at the Q point, we can write,
$\dfrac{{V + 6}}{3} + \dfrac{V}{1} = \dfrac{{9 - V}}{5}$
$ \Rightarrow V\left[ {\dfrac{1}{3} + \dfrac{1}{5} + 1} \right] = \dfrac{9}{5} - 2$
Simplifying the equation further,
$ \Rightarrow V\left[ {\dfrac{{5 + 3 + 15}}{{15}}} \right] = \dfrac{{9 - 10}}{5}$
The potential difference between points Q and P is given by,
$ \Rightarrow V = - \dfrac{1}{5} \times \dfrac{{15}}{{23}} = \dfrac{{ - 3}}{{23}} = - 0.13V$
Thus the current in the 1Ω resistor is ${\text{I = }}\dfrac{{\text{V}}}{{\text{R}}}{\text{ = }}\dfrac{{{\text{0}}{\text{.13}}}}{{\text{1}}}{\text{ = 0}}{\text{.13A}}$.

The current flows from Q to P. The correct answer is Option C.

Note: Kirchhoff's voltage law (KVL) states that the sum of all voltages around any closed loop in a circuit must be equal to zero. This is a consequence of charge conservation and also conservation of energy. This means that the sum of all potential differences across the component involved in the circuit gives a zero reading, as expected.
Assuming potential at Q is $V$, we apply KVL loop 1,
$9 - 2i - 1\left( {i - {i_1}} \right) - 3i = 0$.
When we apply KVL to loop 2,
$6 - 3{i_1} + 1\left( {i - {i_1}} \right) = 0$.
Solving the equations for the two loops,
${\text{i = 1}}{\text{.82A}}$ and ${{\text{i}}_{\text{1}}}{\text{ = 1}}{\text{.95A}}$.
Current through the $1\Omega $ resistor is ${\text{0}}{\text{.13A}}$.