Question

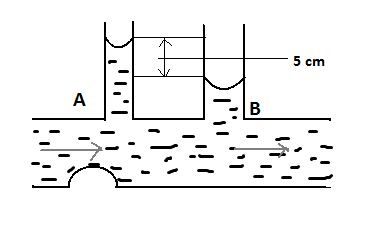
In the diagram shown below, the difference between the tubes of the manometer is 5 cm, the cross-sections at A and B are 6 sq mm and 10 sq mm respectively. The rate at which water flows through the tube is;($g = 10m{\operatorname{s} ^{ - 2}}$)



(A) 7.5 cc/sec
(B) 8.0 cc/sec.
(C) 10.0 cc/sec.
(D) 12.5 cc/sec.

Answer 1

Hint: This problem uses Bernoulli's theorem. Bernoulli's theorem is the pressure version of energy conservation. It is also similar to conservation of momentum.

Complete solution:
Bernoulli’s principle: In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different forms of Bernoulli's equation for different types of flow.
The simplest one being;
$P + \dfrac{1}{2}\rho {v^2} = C$.
Here, $P$ is the pressure at the surface of the liquid due to air, $\rho $ is the density of the fluid and v is the velocity of the fluid and C is constant.
 Bernoulli's theorem also describes the relationship between a fluid's velocity and cross-sectional area. Mathematically it is written as ${A_1}{v_1} = {A_2}{v_2}$.
Now in this case, the difference between the tubes is given viz. 5cm= 0.05 meters.
So first we find the velocity relation in the two tubes.
Hence by applying Bernoulli’s theorem we get;
${A_1}{v_1} = {A_2}{v_2}$ here, ${A_1} = 6m{m^2}$ and ${A_2} = 10m{m^2}$ ;
Thus, $6{v_1} = 10{v_2}$
Thus ${v_1} = \dfrac{5}{3}{v_2}$ (equation:1)
Now apply Bernoulli’s theorem of conservation of pressure;
${P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2$
Solving the equation further we get;
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - {v_1}^2} \right)$
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - \dfrac{{25}}{9}{v_2}^2} \right)$ (from equation: 1)
Now we know that, ${P_2} - {P _1} = \rho g({h_2} - {h_1}) = 0.05\rho g$ (given)
$0.05\rho g = \dfrac{1}{2}\rho \left( {\dfrac{{16}}{9}{v_2}^2} \right)$
Solving the above equation we get,
${v_2} = 0.75m{s^{ - 2}}$
Therefore, rate of flow is mathematically Area X velocity;
Rate=${A_2}{v_2} = 75 \times {10^{ - 1}}c{m^3}{\sec ^{ - 1}}$

Hence option A is correct.

Note: (1) The units must be converted very carefully
(2) Av is the rate of flow of fluid so Bernoulli’s principle states that rate of flow is constant.