
Why in the tetrahedral splitting, terms e and
(A) Due to the approach of the ligands from the axis
(B) Due to the approach of the ligands in between the axis
(C) Due to the symmetry present in the octahedral system
(D) Due to the symmetry present in the tetrahedral system
Answer
146.7k+ views
Hint: If any system is symmetric or has centre of inversion symmetry, it is called gerade orbital, symbolised by g. while if no such symmetry exists, the g term is removed. Octahedral is a symmetric system while tetrahedral is not symmetric.
Complete step-by-step answer:
In an octahedral complex, six ligands are attached to the central transition metal. The d-orbital splits into two different levels. The bottom three energy levels are named as
In a tetrahedral complex, four ligands are attached to the central metal. The d orbitals too split into two different energy levels. The top three consist of the
This difference in ‘g’ terms in both the structure is due to their symmetry. The word g stands for gerade which means symmetry, it is a German word. If the sign of the lobes remains the same, we call it a gerade orbital and if the signs are changed, the orbital is ungerade. In gerade, the centre of inversion symmetry is present.
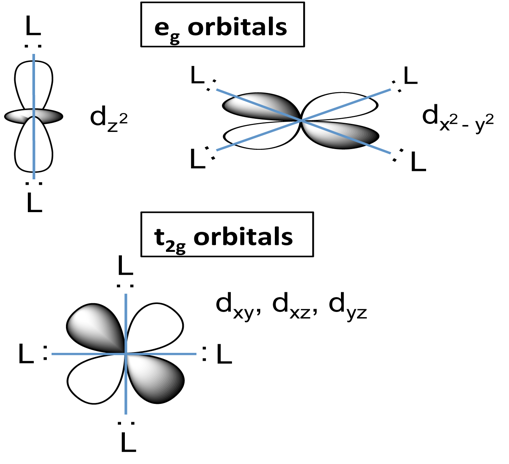
Tetrahedral complexes have no centre of symmetry and thus its orbital do not have g term in it. While in an octahedral system, g term is included because it is symmetric. Therefore, in the tetrahedral splitting, terms e and
Hence, the correct option is (C).
Note: This can also be understood by Laporte selection rule which states that for a coordination complex that contains a centre of symmetry, only transitions which involve a change in parity of lobes are allowed. That is why octahedral is symmetric, hence allowed and vice versa for tetrahedral.
Complete step-by-step answer:
In an octahedral complex, six ligands are attached to the central transition metal. The d-orbital splits into two different levels. The bottom three energy levels are named as
In a tetrahedral complex, four ligands are attached to the central metal. The d orbitals too split into two different energy levels. The top three consist of the
This difference in ‘g’ terms in both the structure is due to their symmetry. The word g stands for gerade which means symmetry, it is a German word. If the sign of the lobes remains the same, we call it a gerade orbital and if the signs are changed, the orbital is ungerade. In gerade, the centre of inversion symmetry is present.

Tetrahedral complexes have no centre of symmetry and thus its orbital do not have g term in it. While in an octahedral system, g term is included because it is symmetric. Therefore, in the tetrahedral splitting, terms e and
Hence, the correct option is (C).
Note: This can also be understood by Laporte selection rule which states that for a coordination complex that contains a centre of symmetry, only transitions which involve a change in parity of lobes are allowed. That is why octahedral is symmetric, hence allowed and vice versa for tetrahedral.
Recently Updated Pages
How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Concept of CP and CV of Gas - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Classification of Drugs

Other Pages
NCERT Solutions for Class 12 Chemistry Chapter 6 Haloalkanes and Haloarenes

NCERT Solutions for Class 12 Chemistry Chapter 2 Electrochemistry

NCERT Solutions for Class 12 Chemistry Chapter 7 Alcohol Phenol and Ether

NCERT Solutions for Class 12 Chemistry Chapter 1 Solutions

Solutions Class 12 Notes: CBSE Chemistry Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs




