Question

In Young’s experiment, the wavelength of red light is \[7800{{\text{A}}^ \circ }\] and that of blue light is $5200{{\text{A}}^ \circ }$. The value of \[n\] which ${({\text{n + 1)}}^{th}}$ blue band coincides with \[{n^{th}}\] red band is
A) 1
B) 2
C) 3
D) 4

Answer 1

Hint: YDSE is Young’s Double Slit Experiment. YDSE is performed with a monochromatic light source.
Coherent source of light: Two sources of light are said to be a coherent source if the phase difference between them is constant and the same frequency.
Monochromatic source of light: The light having the same wavelength is called monochromatic light.
Interference of light: When two monochromatic light waves are superimposed on each other, the intensity in the region of superposition gets redistributed, becoming maximum at some points and minimum at others.

Formula used:
Position of the nth red band, ${{\text{y}}_{{\text{red}}}} = \dfrac{{{\text{nD}}{\lambda _1}}}{{\text{d}}}$,
Position of the ${({\text{n + 1)}}^{th}}$ blue band, ${{\text{y}}_{{\text{blue}}}} = \dfrac{{({\text{n + 1)D}}{\lambda _2}}}{{\text{d}}}$
Here \[\;n = \] number of fringes, \[D = \] the distance of the slit from the screen, \[d = \] distance between the slits,
$\lambda = $ Wavelength of the light source

Complete step by step solution:

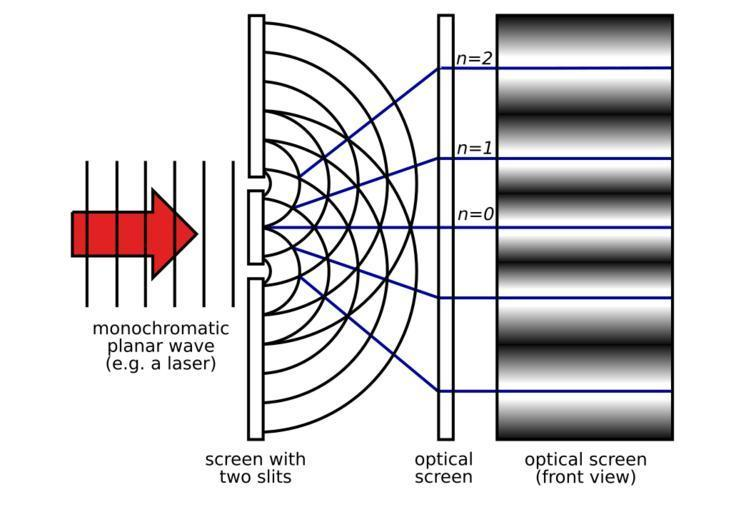
In an interference pattern, the intensities at the points of maxima and minima are directly proportional to the square of the amplitude of the waves.
If there is no interference between the light waves from the two sources, then the intensity at every point will be the same and it will not form any fringes.
According to the question for the coincidence of bands,
We can write it as,
$\dfrac{{{\text{nD}}{\lambda _1}}}{{\text{d}}} = \dfrac{{({\text{n + 1)D}}{\lambda _2}}}{{\text{d}}}$
Canceling the common terms,
We can write as,
${\text{n}}{\lambda _1} = ({\text{n + 1)}}{\lambda _2}$
Now by using the given values,
We can find the value of n,
$7800{\text{n = 5200(n + 1)}}$
On multiplying the RHS term we get,
$ \Rightarrow $$7800{\text{n = 5200n + 5200}}$
Taking the integer as RHS and remaining taken as LHS on subtraction we get,
$ \Rightarrow (7800 - 5200){\text{n = 5200}}$
On subtract we get,
$ \Rightarrow 2600{\text{n = 5200}}$
On divide $2600$ on both side and we get,
$ \Rightarrow {\text{n = }}\dfrac{{{\text{5200}}}}{{2600}}$
$ \Rightarrow {\text{n = 2}}$

Hence the correct option is \[\left( {\text{B}} \right)\].

Note: The intensity of light produced by Young’s Double Slit Experiment is calculated as ${\text{I = }}{{\text{I}}_1} + {{\text{I}}_2}{\text{ + 2}}\sqrt {{{\text{I}}_1}{{\text{I}}_2}} {\text{cos}}\theta $
Bright fringes or constructive interference are produced when the value of ${\text{cos}}\theta {\text{ = 1}}$, $\theta {\text{ = 0, 2}}\pi , 4\pi ,............$
Dark fringes or destructive interference are formed when the value of ${\text{cos}}\theta {\text{ = - 1}}$, $\theta {\text{ = }}\pi {\text{, 3}}\pi {\text{, 5}}\pi ,..............$
According to Huygens’ principle a cylindrical wavefront emerges from a point source, in Young’s Double Slit Experiment point source is used so the wavefronts are cylindrical wavefront.