




How to Calculate Acceleration Due to Gravity with Examples
Acceleration due to gravity is a fundamental concept in physics describing the rate at which objects accelerate towards the Earth due to the gravitational attraction. It serves as a crucial parameter for solving various motion problems in JEE Main Physics and is directly applied in gravitation-related calculations.
Gravitation and Gravity: Fundamental Concepts
Gravitation is the universal force of attraction between any two masses in the universe, acting along the line joining their centers. When one of these masses is the Earth, the force is termed as gravity. Gravity is responsible for objects falling towards Earth's surface and is always directed towards the Earth's center.
The gravitational force between two point masses is given by Newton’s law of universal gravitation:
$F = \dfrac{G m_1 m_2}{r^2}$, where $G$ is the universal gravitational constant, $m_1$ and $m_2$ are the masses, and $r$ is the separation between their centers. For more detailed insight on gravitation, see Gravitation Overview.
Acceleration Due to Gravity ($g$): Definition and Basic Formula
Acceleration due to gravity, represented by $g$, is the acceleration experienced by an object solely under the influence of Earth’s gravitational pull. It is a vector quantity, directed towards the center of the Earth, and is independent of the mass or nature of the object.
At Earth’s surface, $g$ is calculated as:
$g = \dfrac{GM}{R^2}$
where $G = 6.674 \times 10^{-11}\, \dfrac{N\,m^2}{kg^2}$, $M$ is the mass of the Earth $(6 \times 10^{24}\, kg)$, and $R$ is the mean radius of Earth $(6.4 \times 10^6\, m)$.
The standard value of acceleration due to gravity at Earth's surface is approximately $9.8\ m/s^2$. For practical purposes, $g$ may also be expressed as $32\ ft/s^2$ or $980\ cm/s^2$.
Relation Between $g$ and Universal Gravitational Constant $(G)$
By equating the gravitational force and the weight of an object of mass $m$ at Earth's surface:
$mg = \dfrac{GMm}{R^2}$
On simplifying, the expression for $g$ becomes:
$g = \dfrac{GM}{R^2}$
This formula establishes that $g$ depends on the mass of the Earth and inversely on the square of Earth's radius.
Factors Affecting Acceleration Due to Gravity
Acceleration due to gravity is not uniform everywhere on Earth. It varies with height, depth, latitude, rotation, and the Earth’s shape. These variations are significant for analyzing precise motion under gravitation.
Variation of $g$ with Altitude (Height Above Earth's Surface)
The value of $g$ decreases as one moves above Earth's surface. If an object is at height $h$ above the surface, the acceleration due to gravity is given by:
$g_h = \dfrac{GM}{(R + h)^2} = g \left(1 + \dfrac{h}{R}\right)^{-2}$
For $h \ll R$, the binomial expansion gives:
$g_h \approx g \left(1 - \dfrac{2h}{R}\right)$
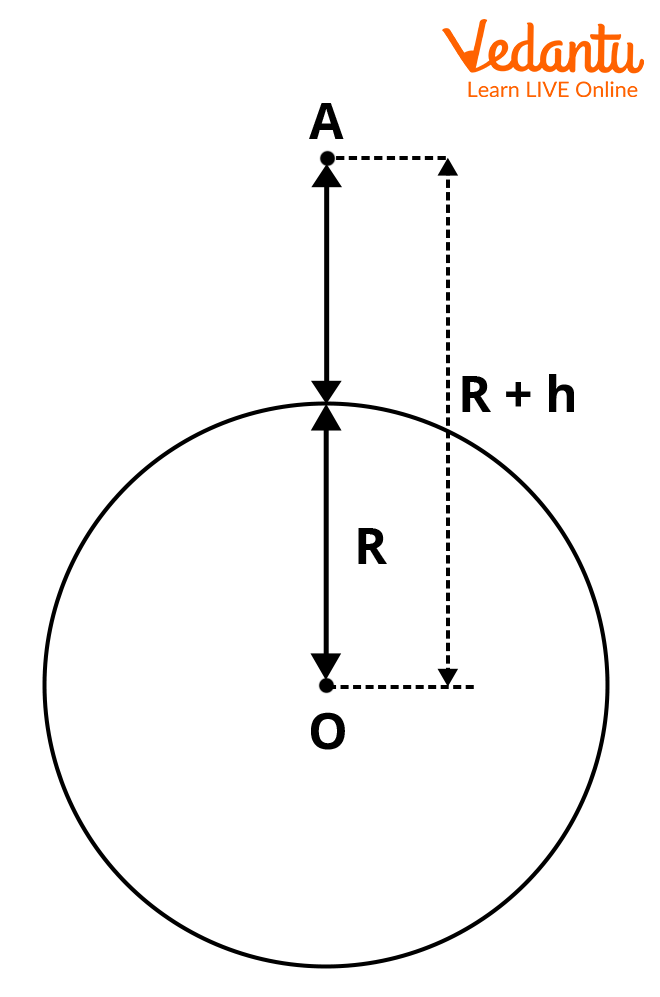
This formula is applied only for heights much smaller than the Earth's radius.
Variation of $g$ with Depth (Below Earth's Surface)
As depth inside the Earth increases, the value of $g$ decreases linearly. At depth $d$ below the surface, the acceleration due to gravity is:
$g_d = g \left(1 - \dfrac{d}{R}\right)$
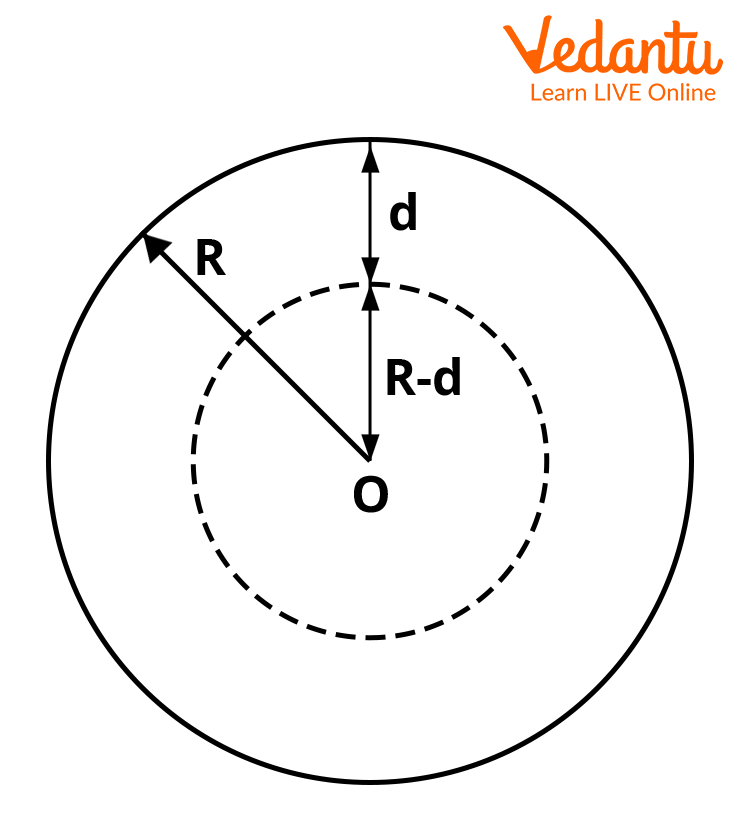
At the center of the Earth $(d = R)$, $g$ becomes zero. This linear decrease contrasts with the quadratic decrease observed for heights above the surface.
Comparative Table: $g$ with Height and Depth
| Position | Value of $g$ |
|---|---|
| At surface | $g$ |
| At height $h$ | $g \left(1 - \dfrac{2h}{R}\right)$ |
| At depth $d$ | $g \left(1 - \dfrac{d}{R}\right)$ |
| At center | $0$ |
Comparison of Height and Depth for Equal Change in $g$
For small changes, the decrease in $g$ at height $h$ above Earth's surface equals the decrease at depth $d = 2h$ below the surface. This relationship helps in solving comparative problems in JEE examinations.
Variation of $g$ due to Earth's Rotation
Earth’s rotation causes a reduction in apparent gravity, especially near the equator. The effective acceleration due to gravity is given by:
$g_{eff} = g - \omega^2 R \cos^2\lambda$
Here, $\omega$ is Earth’s angular velocity and $\lambda$ is the latitude. The effect is maximum at the equator $(\lambda = 0^\circ)$ and zero at the poles $(\lambda = 90^\circ)$.
Variation of $g$ due to Earth's Shape
Earth is an oblate spheroid, flattened at the poles and bulged at the equator. The polar radius is less than the equatorial radius, so gravity is slightly greater at the poles than at the equator. The change is about $0.5\%$.
Therefore, the value of $g$ is maximum at the poles and minimum at the equator.
Acceleration Due to Gravity on Celestial Bodies
The acceleration due to gravity differs on various celestial objects, as it depends on their mass and radius. For example, $g$ on the Moon is about $1.62\ m/s^2$, and on Mars it is around $3.71\ m/s^2$, both significantly less than Earth's value.
For questions involving gravitation on other planets, see Gravitation Mock Test 1.
Units and Dimensional Formula of $g$
The SI unit of acceleration due to gravity is $m/s^2$. In some cases, it may also be expressed in $ft/s^2$ or $in/s^2$ depending on the chosen unit system. The dimensional formula for $g$ is $[M^0LT^{-2}]$.
Solved Example: Acceleration Due to Gravity with Height
If $g$ at Earth's surface is $9.8\ m/s^2$, calculate $g$ at a height $h$ where $h = 0.05R$.
- $g = 9.8\ m/s^2$
- $h = 0.05R$, $R = $ Earth's radius
- $g_h = g (1 - \dfrac{2h}{R}) = 9.8 \times (1 - 0.1) = 8.82\ m/s^2$
Solved Example: Acceleration Due to Gravity with Depth
An object is placed at a depth $d = 1600$ km inside Earth. Find the acceleration due to gravity if $R = 6400$ km and $g = 9.8\ m/s^2$ at the surface.
- $g_d = g (1 - \dfrac{d}{R})$
- $g_d = 9.8 \times \left(1 - \dfrac{1600}{6400}\right) = 9.8 \times 0.75 = 7.35\ m/s^2$
Importance of $g$ in Physics Problems
The value and variations of $g$ influence the motion of falling bodies, projectile motion, weight measurements, and energy calculations. Mastery of these concepts is essential for strong performance in JEE examinations.
For understanding gravitational potential and its link with $g$, refer to Gravitational Potential Energy.
Key Points on Acceleration Due to Gravity
- Standard value of $g$ on Earth is $9.8\ m/s^2$
- $g$ decreases with altitude and depth inside Earth
- Earth’s rotation and shape cause variations in $g$
- $g$ is maximum at the poles and minimum at the equator
- $g$ on Moon and Mars is less than on Earth
- $g$ is a vector, always directed to Earth's center
Practice Further on Acceleration Due To Gravity
To enhance your understanding, solve additional problems from Acceleration Due To Gravity, Gravitation Mock Test 2, and Gravitation Mock Test 3.
FAQs on What Is Acceleration Due to Gravity?
1. What is acceleration due to gravity?
Acceleration due to gravity is the rate at which an object accelerates when freely falling towards the Earth due to its gravitational pull.
- Denoted by g
- Standard value on Earth is 9.8 m/s²
- Acts towards the centre of the Earth
- Key term in mechanics and Newton’s Laws
- Relevant for CBSE Physics exams and numerical problems
2. What is the formula for acceleration due to gravity?
The formula for acceleration due to gravity is:
- g = GM/R²
Where:
- G = Universal Gravitational Constant (6.67 × 10⁻¹¹ Nm²/kg²)
- M = Mass of the Earth
- R = Radius of the Earth
This formula is vital for CBSE syllabus and numericals.
3. Does acceleration due to gravity change with height and depth?
Yes, acceleration due to gravity (g) decreases as height above Earth's surface increases and also decreases as you go deeper inside Earth.
- At greater heights: g decreases
- At greater depths (but not centre): g decreases
This concept is important for understanding variations in gravitational force for examinations.
4. What factors affect acceleration due to gravity?
The value of g is affected by several factors:
- Mass of the Earth: Directly proportional
- Radius of the Earth: Inversely proportional (g ∝ 1/R²)
- Altitude (height above surface): g decreases with height
- Depth inside Earth: g decreases with depth
- Latitude: Slightly varies due to Earth's shape
These are frequent exam questions in the CBSE Physics syllabus.
5. What is the difference between gravity and gravitation?
Gravity refers specifically to the attraction between the Earth and objects near its surface, while gravitation is the universal force of attraction between any two masses.
- Gravity: Specific to Earth’s pull
- Gravitation: Any two objects in the universe
- Both are based on Newton's Law of Universal Gravitation
6. Why is acceleration due to gravity different at different places on Earth?
Acceleration due to gravity (g) is different at different places because the Earth is not a perfect sphere and its density varies.
- Poles: g is maximum
- Equator: g is minimum
- Difference due to Earth's rotation and bulging at the equator
This is a key point in CBSE exams and helps explain weight variations globally.
7. How does the value of g on the Moon compare with that on Earth?
The value of acceleration due to gravity (g) on the Moon is about 1/6th that on Earth.
- Earth: g = 9.8 m/s²
- Moon: g ≈ 1.62 m/s²
- This is due to the Moon’s smaller mass and radius, explained using the formula g = GM/R²
8. What is the value of acceleration due to gravity on Earth and why?
On the Earth’s surface, the standard value of acceleration due to gravity is 9.8 m/s².
- Depends on Earth’s mass and radius
- Calculated using g = GM/R²
- Average value; varies slightly from place to place
9. Why do objects of different masses fall at the same rate in the absence of air resistance?
In the absence of air resistance, all objects fall at the same rate because acceleration due to gravity (g) is independent of mass.
- Galileo proved this using experiments
- Formula shows g has no term for falling object's mass
- Relevant for practical and theoretical questions in CBSE Physics
10. What is the Universal Gravitational Constant (G)?
The Universal Gravitational Constant (G) is a constant of proportionality in Newton’s Law of Universal Gravitation.
- Value: 6.674 × 10⁻¹¹ N·m²/kg²
- Same value everywhere in the universe
- Used in the calculation of acceleration due to gravity
- Important for CBSE Physics formulae and numericals
11. How is the weight of an object related to acceleration due to gravity?
The weight (W) of an object is the force with which it is attracted towards the Earth, calculated by multiplying its mass (m) by acceleration due to gravity (g).
- Weight (W) = mass (m) × acceleration due to gravity (g)
- SI unit: Newton (N)
- Synonymous keywords: force, mass, gravity
12. Why does acceleration due to gravity have a negative sign in equations?
Acceleration due to gravity is often assigned a negative sign in equations because it acts downward, towards the centre of the Earth.
- Follows standard convention for direction
- Negative sign helps in vector calculations and numericals
:strong>g is always directed downwards in calculations

































