




How Kinetic and Potential Energy Interact in SHM
Energy in simple harmonic motion (SHM) is a fundamental aspect of oscillatory systems in physics. SHM describes the periodic back-and-forth motion of a particle, where energy continuously shifts between kinetic and potential forms while the total mechanical energy remains constant throughout the motion.
Potential Energy in Simple Harmonic Motion
In SHM, potential energy arises due to the displacement of the particle from its equilibrium position. The restoring force can be represented as $F = -k x$, where $k$ is the force constant and $x$ is the displacement. The potential energy at displacement $x$ is given by $U = \dfrac{1}{2} k x^2$.
Since the relation $k = m \omega^2$ holds for SHM, the potential energy can also be written as $U = \dfrac{1}{2} m \omega^2 x^2$, where $m$ is the mass and $\omega$ is the angular frequency.
The potential energy is maximum at the extreme positions of the oscillation, where displacement is equal to the amplitude $A$. At $x = A$, $U_{max} = \dfrac{1}{2} m \omega^2 A^2$.
Kinetic Energy in Simple Harmonic Motion
Kinetic energy in SHM is due to the velocity of the particle as it moves through its path. The velocity at any displacement $x$ is described by $v = \omega \sqrt{A^2 - x^2}$, where $A$ is the amplitude. The kinetic energy is then given by $K = \dfrac{1}{2} m v^2 = \dfrac{1}{2} m \omega^2 (A^2 - x^2)$.
At the mean position $(x = 0)$, the kinetic energy reaches its maximum value $K_{max} = \dfrac{1}{2} m \omega^2 A^2$. At the extreme positions $(x = \pm A)$, the kinetic energy becomes zero as the particle momentarily comes to rest.
Total Mechanical Energy in Simple Harmonic Motion
The total mechanical energy $E$ of a particle in SHM is the sum of its kinetic and potential energies at any instant. Substituting the expressions:
$E = K + U = \dfrac{1}{2} m \omega^2 (A^2 - x^2) + \dfrac{1}{2} m \omega^2 x^2 = \dfrac{1}{2} m \omega^2 A^2$
This result shows that the total energy in SHM is independent of displacement $x$, and remains constant throughout the motion, provided no dissipative forces are present.
In terms of frequency $f$, using $\omega = 2\pi f$, the total energy can be written as $E = 2\pi^2 m f^2 A^2$.
To study the mathematical formulation of oscillations, see Simple Harmonic Motion.
Variation of Energy with Displacement
During SHM, kinetic and potential energies continuously convert into one another as the particle oscillates. At equilibrium position $(x = 0)$, the entire energy is kinetic, while at extreme positions $(x = \pm A)$, the entire energy is potential.
At any intermediate position, both kinetic and potential energies are non-zero, and their sum remains constant. The energy variations as functions of displacement are given by:
- Kinetic energy decreases as displacement increases
- Potential energy increases with displacement from equilibrium
- Total energy remains constant for all values of displacement
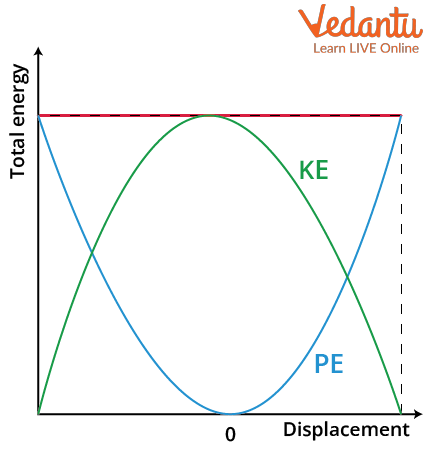
Graphical Representation of Energies in SHM
The graphs of kinetic and potential energies against displacement are parabolic in nature. The total energy graph appears as a straight line parallel to the displacement axis, indicating that it does not vary with position. The potential energy curve opens upwards, while the kinetic energy curve opens downwards with respect to displacement.
Study additional topics on periodic motion and energy transformations in related chapters such as Oscillations And Waves.
Frequency of Energy Variation in SHM
The kinetic and potential energies in SHM vary between zero and their maximum values during the motion. Both energies complete two full cycles in the time the displacement completes one. Hence, the frequency of variation of kinetic or potential energy is twice the frequency of the oscillation.
If the displacement is $x = A \cos(\omega t)$, the kinetic energy is $K = \dfrac{1}{2} m \omega^2 A^2 \sin^2(\omega t)$. Since $\sin^2(\omega t)$ completes two cycles in the period $T$, the energy varies with frequency $2f$.
Key Points on Energy in SHM
- Total mechanical energy depends on mass, frequency, and amplitude
- Potential energy is maximum at extreme displacements
- Kinetic energy is maximum at the mean position
- Total energy remains constant if there is no dissipation
- Frequency of variation of energy is double that of displacement
Illustrative Example: Energy Calculations in SHM
Consider a particle of mass $0.2\, \mathrm{kg}$ executing SHM with amplitude $0.05\, \mathrm{m}$ and frequency $1\, \mathrm{Hz}$. Find the total energy and maximum kinetic energy.
| Physical Quantity | Value |
|---|---|
| Mass ($m$) | $0.2\, \mathrm{kg}$ |
| Amplitude ($A$) | $0.05\, \mathrm{m}$ |
| Frequency ($f$) | $1\, \mathrm{Hz}$ |
| Angular frequency ($\omega$) | $2\pi f = 2\pi\, \mathrm{rad/s}$ |
| Total energy ($E$) | $2\pi^2 m f^2 A^2 = 2\pi^2 \times 0.2 \times 1^2 \times (0.05)^2$ |
| Numerical value ($E$) | $0.00987\, \mathrm{J}$ |
The value calculated gives the total energy of the system, which is equal to the maximum kinetic and maximum potential energy in SHM.
Review further applications of work and energy in oscillatory systems in Work Energy And Power.
Practical Examples of Energy in SHM
- Oscillation of a spring-mass system
- Pendulum motion near equilibrium
- Vibrations of a guitar string
- Molecules undergoing vibrational energy exchange
Study the application of SHM to mechanical systems in the Spring Mass System chapter.
Summary of Energy Relationships in SHM
In simple harmonic motion, the energy transformations between kinetic and potential forms demonstrate the conservative nature of the force involved. The total mechanical energy is solely determined by the mass, angular frequency, and amplitude of oscillation, and is independent of time or displacement.
For a conceptual understanding of thermal motions and kinetic concepts, refer to Kinetic Theory Of Gases and other foundational physics topics.
FAQs on Understanding Energy in Simple Harmonic Motion
1. What is the total energy in simple harmonic motion (SHM)?
Total energy in simple harmonic motion (SHM) is the sum of kinetic and potential energies and remains constant for an ideal system.
- The total mechanical energy (E) in SHM is given by E = (1/2) m ω² A², where m is mass, ω is angular frequency, and A is amplitude.
- Kinetic energy and potential energy continuously convert into each other during the motion, but their sum stays the same.
2. How is energy distributed in simple harmonic motion?
Energy in simple harmonic motion is shared between kinetic and potential energy depending on position.
- At the mean position: Kinetic energy is maximum, potential energy is minimum (zero for spring SHM).
- At extreme positions: Potential energy is maximum, kinetic energy is zero.
- Throughout the oscillation, energy continuously shifts between kinetic and potential forms, but the total remains constant.
3. What is the expression for kinetic energy in SHM?
Kinetic energy in SHM depends on both the mass, angular frequency, amplitude, and position of the particle.
- The kinetic energy (KE) at displacement x is given by: KE = (1/2) m ω² (A² - x²)
- KE is maximum at mean position (x = 0) and zero at extreme positions (x = ±A).
4. What is the potential energy in simple harmonic motion?
Potential energy in SHM represents the stored energy due to displacement from the mean position.
- The expression is: PE = (1/2) m ω² x²
- Potential energy is zero at the mean position and maximum at the extremes (x = ±A).
5. Why is total energy conserved during simple harmonic motion?
Total energy is conserved in SHM because there are no external or non-conservative forces acting.
- In the absence of friction or damping, the sum of kinetic and potential energies remains constant.
- This conservation allows for continuous oscillation at constant amplitude and frequency.
6. How do kinetic and potential energies vary in SHM?
Kinetic and potential energies in SHM vary sinusoidally and interchange during motion.
- Kinetic energy is highest at the mean position (x = 0).
- Potential energy is highest at extreme positions (x = ±A).
- At any instant: KE + PE = Total energy
7. How is energy calculated for a mass-spring system in SHM?
Energy for a mass-spring system in SHM is determined by its amplitude and spring constant.
- Total energy (E) = (1/2) k A², where k is the spring constant and A is the amplitude.
- This formula is derived from the maximum potential or kinetic energy during oscillation.
8. What happens to the energy of a damped oscillator?
Energy of a damped oscillator gradually decreases with time due to non-conservative forces like friction.
- The amplitude of oscillations reduces over time, and total energy is lost as heat or sound.
- This is different from ideal SHM, where total energy remains constant.
9. At what point is the potential energy maximum in SHM?
Potential energy is maximum at the extreme positions of SHM.
- At these points, the entire energy of the particle is stored as potential energy.
- Kinetic energy is zero at maximum displacement (x = ±A).
10. Is mechanical energy always conserved in SHM?
Mechanical energy is conserved in SHM if there are no dissipative forces present.
- Ideal SHM assumes no friction or air resistance, ensuring energy conservation.
- In real systems, some energy may be lost, leading to damped oscillations.
























