




How is the Magnetic Field Derived Inside a Toroid?
The study of the magnetic field due to a toroid is essential for understanding magnetic effects in current-carrying conductors, especially in circular geometries. The toroid is a fundamental element in electromagnetism, frequently applied in inductors, transformers, and advanced circuits. In this article, the magnetic field characteristics of a toroid, its mathematical derivation, physical properties, and comparison with solenoids are discussed in detail.
Definition and Construction of a Toroid
A toroid is a ring-shaped coil formed by winding a conducting wire closely and uniformly on a circular core. The windings are kept very close to minimize field leakage and to confine the magnetic field within the core. Toroids are widely used as inductive elements in electronic circuits that require minimal electromagnetic interference. For more concepts on magnetic fields produced by current-carrying conductors, refer to Magnetic Effects of Current.
Ampere’s Circuital Law and Its Application to Toroids
Ampere’s Circuital Law states that the line integral of the magnetic field $\vec{B}$ around any closed path is equal to $\mu_0$ times the total current enclosed by the path. This law provides the mathematical foundation for deriving the magnetic field inside a toroid. The law is expressed as: $\oint \vec{B} \cdot d\vec{l} = \mu_0 I_{enc}$ where $\mu_0$ is the permeability of free space, and $I_{enc}$ is the net current enclosed.
Derivation of Magnetic Field Due to a Toroid
Consider a toroid with $N$ turns, each carrying current $I$. The toroid has a mean radius $r$. Applying Ampere’s Law to a circular path of radius $r$ inside the core, the magnetic field $B$ is tangential and constant in magnitude along the path. $\oint \vec{B} \cdot d\vec{l} = B \oint d l = B \cdot 2\pi r$ The net current enclosed by the Amperian loop is $NI$, since there are $N$ turns. Applying Ampere’s Law: $B \cdot 2\pi r = \mu_0 N I$ $B = \dfrac{\mu_0 N I}{2\pi r}$ This expression gives the magnetic field at a distance $r$ from the center inside the toroid.
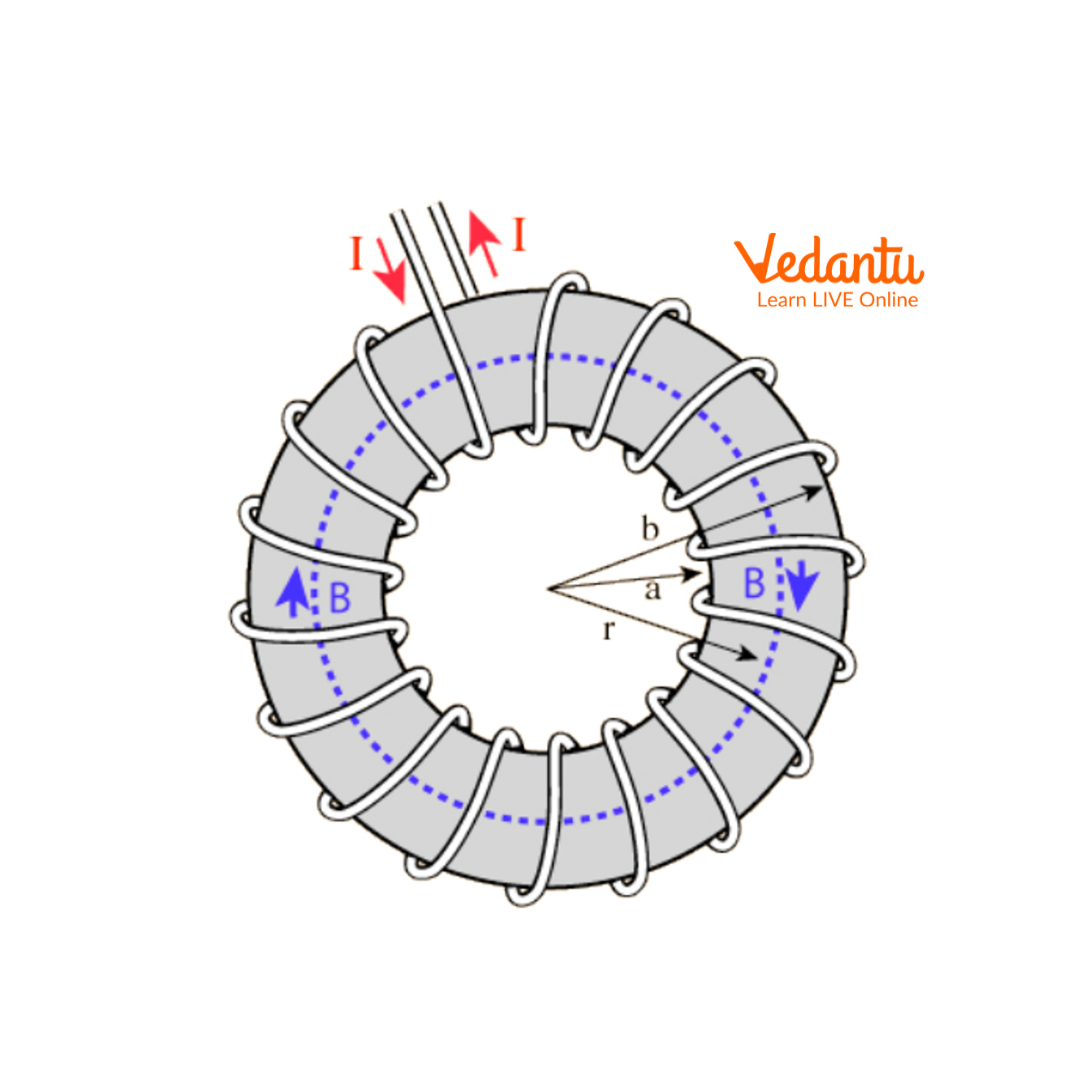
The magnetic field is nearly confined to the core of the toroid and is tangential at every point inside. The field outside the toroid and at its center is approximately zero due to the closed-loop nature of the windings. For more details on calculating flux in such configurations, refer to Flux and Magnetic Field.
Variation and Uniformity of Magnetic Field in a Toroid
The magnetic field inside a toroid is inversely proportional to the radius $r$ from the center. This means the field is not perfectly uniform across the cross-section unless the toroid is very thin (i.e., the difference between the inner and outer radius is small). The field remains nearly zero outside the coil and at the toroid's central void.
Calculation of Number of Turns in a Toroid
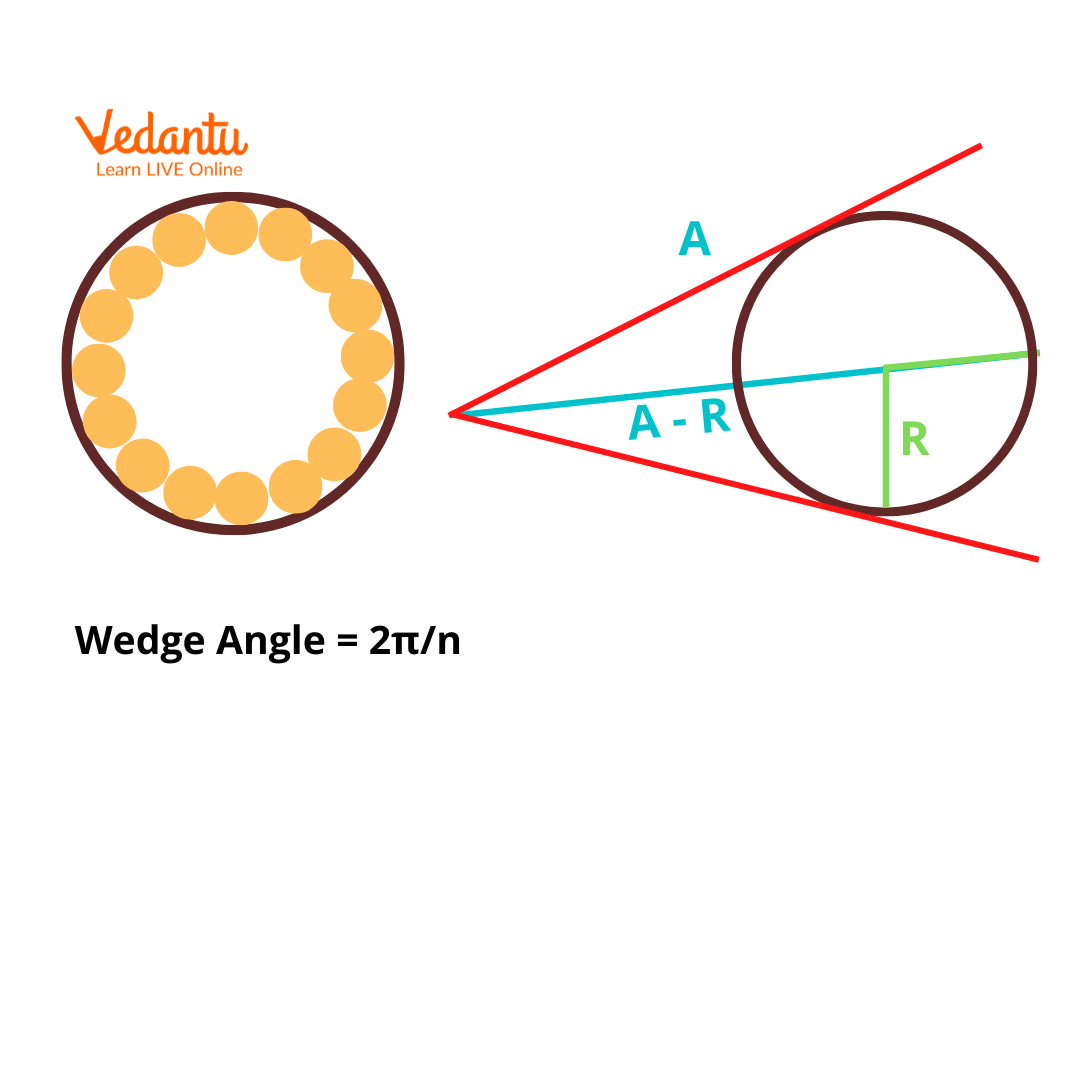
Let $R$ denote the radius of the winding wire, $n$ the total number of loops, and $A$ the inner radius of the toroid. The wedge angle for each turn is $2\pi/n$ radians. The relationship among these parameters is described by: $\sin \dfrac{\pi}{n} = \dfrac{R}{A - R}$ This equation allows for the calculation of the number of turns based on geometric constraints of the toroid.
Inductive Behavior and Properties of a Toroid
Toroids act as inductors in electrical circuits. When current changes through a toroid, the time-varying magnetic flux induces an opposing electromotive force (emf). The confined magnetic field leads to low electromagnetic interference. Basic properties of toroids are summarized below.
- Closed-loop windings produce high inductance
- Magnetic field is strong and confined within the core
- Electromagnetic interference is minimized
Magnetic Field Due to Toroidal Solenoid
A toroidal solenoid is a specialized toroid with many closely wound turns. The magnetic field inside is given by the same formula as a general toroid: $B = \dfrac{\mu_0 N I}{2\pi r}$ The field at the center and outside remains negligible. The field inside does not depend on the material surrounding the toroid but only on the number of turns, current, and mean radius. For a detailed analysis, see Magnetic Field Due to Toroid.
Principle and Application of Toroidal Transformers
Toroidal transformers utilize toroids as their core to achieve efficient power transfer with minimal core losses. Alternating current in the primary winding produces an alternating magnetic flux, which induces an emf in the secondary coil through mutual induction. This principle is extensively used in electronic devices that require transformers with high efficiency and low electromagnetic emission. To understand more about electromagnetic induction, refer to Electromagnetic Induction Notes.
Comparison of Toroid and Solenoid
Toroids and solenoids are both based on the concept of current-induced magnetic fields. However, their geometrical configurations lead to different magnetic field distributions and applications. The following table highlights their differences for clarity.
| Property | Toroid |
|---|---|
| Shape | Circular (ring-shaped) |
| Magnetic field location | Inside core |
| Field outside/center | Nearly zero |
| Field uniformity | Non-uniform |
| Inductive efficiency | High (closed-loop system) |
Enhancing Magnetic Field Inside a Toroid
The magnetic field inside a toroid can be enhanced by increasing the number of turns, raising the current, or reducing the mean radius. Utilizing a core material with high permeability also increases the effective field. For detailed study of self and mutual inductance, visit Self-Inductance or Mutual Inductance.
FAQs on Understanding the Magnetic Field Due to a Toroid
1. What is a toroid in physics?
A toroid is a coil of wire wound in a circular shape, forming a closed loop similar to a donut. It is used to study and generate uniform magnetic fields in electromagnetism experiments. Key features include:
- Closed magnetic path
- Wire wound on a doughnut-shaped core, commonly made of iron
- Used in inductors, transformers, and magnetic field experiments
2. What is the magnetic field inside a toroid?
The magnetic field inside a toroid is uniform and given by the formula:
B = (μ₀ × n × I), where μ₀ is the permeability of free space, n is the number of turns per unit length, and I is the current. Important points:
- The field is strongest within the core
- Field lines form concentric circles inside the toroid
- Outside and at the center, the magnetic field is nearly zero
3. Why is there no magnetic field outside a toroid?
There is virtually no magnetic field outside a toroid because the circular loop of the winding creates a confined magnetic field within the core. This happens due to:
- Symmetrical winding of wire
- Magnetic field lines forming closed loops inside
- External fields from each segment cancel out
4. How do you derive the expression for magnetic field due to a toroid using Ampere’s Law?
To derive the magnetic field inside a toroid using Ampere’s Law, follow these steps:
- Consider a circular Amperian loop inside the toroid’s core
- Apply Ampere’s circuital law: ∮B·dl = μ₀I_enclosed
- B × (2πr) = μ₀ × n × I × (2πr)
- Solve to get B = μ₀nI
5. What are the applications of a toroid?
A toroid is widely used in electrical engineering and physics due to its well-confined magnetic field. Common applications include:
- Transformers and inductors
- Magnetic field sensors
- Electromagnetic shielding
- Particle accelerators and fusion research
6. How does a toroid differ from a solenoid?
A toroid and a solenoid both create magnetic fields, but a toroid has its coil wound in a circular shape, forming a closed magnetic path. Key differences:
- Shape: Toroid is donut-shaped; solenoid is cylindrical
- Magnetic Field: Toroid’s field is inside the core; solenoid’s field spills out on the ends
- Magnetic Field Outside: Negligible for toroid, significant for solenoid
7. What is the formula for calculating the magnetic field at a distance r from the center of a toroid?
The magnetic field at a radius r inside a toroid is calculated by:
B = (μ₀ × N × I) / (2πr)
- μ₀ = Permeability of free space
- N = Total number of turns
- I = Current through the winding
- r = Distance from the center of the toroid
8. What is the direction of the magnetic field in a toroid?
The magnetic field inside a toroid forms concentric circles along the core and follows the right-hand rule. Key points:
- Direction depends on current direction
- Field circulates within the core
- Reverse current reverses the magnetic field direction
9. What factors affect the strength of the magnetic field inside a toroid?
The strength of the magnetic field inside a toroid depends on several factors:
- Number of turns of coil (N or n)
- Current (I) passing through the winding
- Permeability of the core material (μ₀ or μ)
- Radius (r) of the toroid
10. What are the advantages of using a toroid in practical applications?
Using a toroid in electrical circuits has several advantages:
- Provides confined, leak-proof magnetic fields
- Minimizes electromagnetic interference
- Reduces losses due to external field leakage
- Improves energy efficiency in inductive devices
























