Malus Law: Understanding the Intensity of Polarised Light for JEE Main 2025
Malus' Law is a fundamental concept in optics that describes the intensity of polarised light passing through a polarising filter. This law is crucial for understanding the behaviour of light as it interacts with polarisers and is an important topic for the JEE Main 2025 exam.
In this section, we will explore the formula for Malus' Law, its derivation, and real-world applications. Understanding this law is essential for solving problems related to polarization, which frequently appear in competitive exams like JEE Main.
What is Malus Law?
Malus law deals with the polarization properties of light. It helps us to study the relation of the intensity of light and the polarizer-analyzer.
The law was derived by Etienne-Louis Malus in 1808. He discovered that natural light could be polarized when reflected by a glass surface. He used a calcite crystal to conduct his experiment.
After conducting the experiment, he observed that two types of polarization occurred in natural light that is s- and p- polarization, which are mutually perpendicular to each other.
This law is used to relate the intrinsic connection between optics and electromagnetism. This law also demonstrates the transverse nature of electromagnetic waves.
Malus observed that the intensity varied from maximum to minimum when the crystal was rotated. Accordingly, he proposed that the amplitude of reflected ray must be A = A0 cosθ. Malus squared the amplitude relation in order to obtain the intensity. Hence, the intensity equation I(θ) of the reflected polarized light is given by the following equation,
$I = I_0 \cos^2 \phi$
Where,
$I_0 = A_0^2$
This equation is known as Law of Malus Equation. The figure represents a normalized plot of Malus’s Law.
State Malus Law
It states that the intensity of plane-polarized light that passes through an analyzer varies directly with the square of the cosine of the angle between the plane of the polarizer and the transmission axes of the analyzer.
Image state malus law
Derive Malus Law
Let θ be the angle between the transmission axes of the analyzer and the polarizer. The plane-polarized light that emerges from the polarizer is incident on the analyzer. The intensity of the incident light on the analyzer ‘I0’ is directly proportional to the square of the amplitude of the electric vector ‘E0’.
I ∞ E02
Two rectangular components viz: E0cosθ and E0sinθ can be derived from the electric field E0. Here the electric vector E0cosθ that is parallel to the transmission axis gets transmitted through the analyzer.
The component of the electric vector E0sinθ will be absorbed by the analyzer. The intensity ‘I’ of light transmitted by the analyzer is,
I ∝ (E0 x cosθ)2
Hence,
I / I0 = (E0 x cosθ)2/E02 = cos2θ
I = I0 x cos2θ
Therefore,
I ∝ cos2θ
The above equation proves the Law of Malus Equation.
Malus Law Experiment
Aims and Objective: The aims and objectives of this experiment are to identify the relationship between the intensity of light transmitted through the analyzer and the angle ‘𝜃′ between the axes of the polarizer and analyzer.
Apparatus Used: Requirements of the experiment are:
A diode laser
Photodetector
Polarizer-analyzer pair
Output measuring unit (microammeter)
A dial fitted with the polarizer, and
Optical bench.
Malus Law Formula
The transmitted light's intensity is given by the formula:
\[I_{t} = A_{t}^{2} = A_{o}^{2} Cos^{2}\theta = I_{o} Cos^{2}\theta \]
Where,
It = intensity of light transmitted through the analyzer;
Io = intensity of the incident plane-polarized light l, and
θ = angle between the axis of the polarizer and analyzer
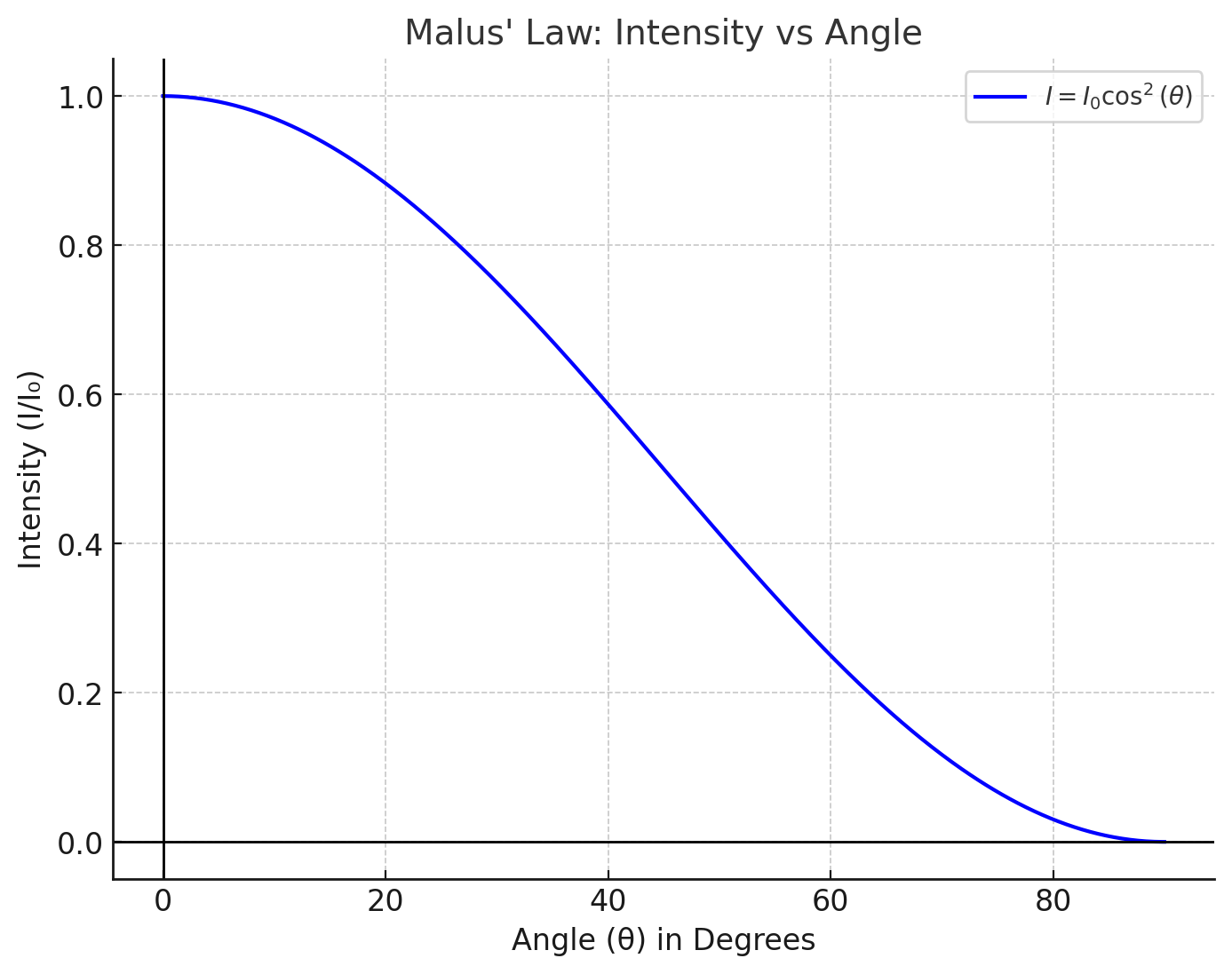
Malus Law Graph
Here is the Malus Law Graph. It shows the relationship between the intensity of transmitted light and the angle $\theta$ between the polarization direction of light and the axis of the polarizer. The graph follows the equation $I = I_0 \cos^2(\theta)$, with intensity varying from maximum to minimum as the angle changes from 0° to 90°.
Theory
Sunlight, candlelight, and the light emitted by an electric bulb is ordinary light and are called unpolarized light. The magnetic and electric fields vibrate in all possible directions perpendicular to each other and also perpendicular to the direction of propagation of the light in unpolarized light.
The unpolarized light is represented in figure- 1(a). The unpolarized light is considered to be composed of two linear and orthogonal polarization states with complete incoherence.
When unpolarized light is incident on a polarizer, the intensity of transmitted light from the polarizer reduces to one-half of the incident light.
Also, no change in the irradiance of the transmitted light occurs if the polarizer is rotated with respect to the incident light, and its intensity remains the same as half of the incident light.
Polarization
Some transparent materials like Nicol and Tourmaline are capable of filtering light, thereby allowing light waves with vibrations in only one place. Such material is called Polaroids.
The filtration of light is possible only because of the structure of the material, which has its cells arranged in a straight line and in a direction parallel to the axis of the polarizer. (Represented in figure 1 (b) and 1( c).)
The phenomenon of filtration of light waves and producing it with vibrations in a single direction is called polarization. Polarization is the property of a material by which it filtrates light and makes it directional.
Discussion
The current for different angles of rotation of the analyzer makes a cosine curve of 360° rotation. It indicates the validity of the equation. The experimentally measured current (Iexpt) and (Itheo) that were calculated using equation Itheo = Imax Cos2θ is within the limits of error.
The relative intensity of light that comes out from the analyzer is maximum at 0° and 180°. It attains a minimum value of 90° and 270°. The cosine values vary as per the graph between those values.
The curve of light intensity Iexpt versus Cos2θ is a straight line with a unit slope, which indicates the correctness of Malus's law.
Application of Malus Law
Malus Law plays a crucial role in understanding the behaviour of polarized light and has several practical applications in various fields. Here are some Applications of Malus Law:
Polarization of Light: Malus' Law helps explain how light can be polarized when passing through a polarizing filter.
Optical Instruments: In instruments such as polarimeters, Malus' Law is used to measure the polarization of light.
Sunglasses and Camera Filters: Polarizing filters in sunglasses and camera lenses utilize Malus' Law to reduce glare.
Stress Analysis in Transparent Materials: Malus' Law is applied in photoelasticity, a technique used to study stress distribution in transparent materials.
Liquid Crystals and LCD Screens: Malus' Law is also fundamental in the working of liquid crystal displays (LCDs). Liquid crystal molecules align in response to electric fields, affecting the polarization of light passing through them. By adjusting the polarization angles, the intensity of light can be controlled, allowing for the creation of images on the screen.
Malus Law Example:
1. Monochromatic light of intensity $I_0$ passes through a polarizer. If the intensity of light emerging from the polarizer is I, what will be the angle between the transmission axis of the polarizer and the vibration direction of the incident light?
Solution:
Malus' Law is given by $I=I_0 \cos ^2 \theta$, where $I$ is the intensity of light after passing through a polarizer, $I_0$ is the initial intensity, and $\theta$ is the angle between the transmission axis and the vibration direction.
Rearranging the equation for $\theta$ :
$\cos ^2 \theta=\frac{I}{I_0} $
$\theta=\cos ^{-1} \sqrt{\frac{I}{I_0}}$
2. Light of intensity $9 I_0$ passes through two ideal polarizers. If the angle between the transmission axes of the two polarizers is $60^{\circ}$, find the intensity of light emerging from the second polarizer.
Solution:
Using Malus' Law twice, the intensity $I$ after passing through two polarizers is given by: $I=I_0 \cos ^2 \theta_1 \cos ^2 \theta_2$
where $\theta_1$ is the angle between the initial light polarization direction and the first polarizer's transmission axis, and $\theta_2$ is the angle between the two polarizers' transmission axes.
Given $I=9 I_0$ and $\theta_2=60^{\circ}$, you can find $\theta_1$ and then substitute the values into the formula to get the final intensity.
3. A beam of polarized light with intensity $I_0$ passes through two polarizing sheets. If the first sheet is rotated by an angle $\theta_1$ and the second sheet by an angle $\theta_2$, find the intensity of light emerging from the second sheet.
Solution:
The intensity $I$ after passing through two polarizers is given by:
$I=I_0 \cos ^2\left(\theta_1-\theta_2\right)$
This formula is derived by considering the angles between the incident light and the first polarizer $\left(\theta_1\right)$ and between the first polarizer and the second polarizer $\left(\theta_2\right)$.
4. A beam of light is incident on a polarizer with an intensity $I_0$. If the polarizer is rotated by an angle $\alpha$, find the new intensity of the transmitted light.
Solution:
The intensity $I$ after rotating the polarizer is given by:
$I=I_0 \cos ^2 \alpha$
This equation comes directly from Malus' Law, where $\alpha$ is the angle between the original transmission axis and the new transmission axis.
5. Light of intensity $I_0$ passes through a polarizer. If the transmitted light then passes through another polarizer whose transmission axis makes an angle $\theta$ with the original transmission axis, find the intensity of the final transmitted light.
Solution:
The intensity $I$ after passing through two polarizers is given by:
$I=I_0 \cos ^2 \theta$
Here, $\theta$ is the angle between the transmission axes of the two polarizers. Simply plug in the given values to find the final intensity.
Conclusion
Malus Law is a crucial concept in physics, particularly for JEE Main preparation. It explains how light intensity changes when unpolarized light passes through a polaroid. The law states that the intensity of polarized light is proportional to the square of the cosine of the angle between the polarizer and the light's original direction. This mathematical relationship helps analyze and understand the behaviour of polarized light, making it valuable in optics. Mastering Malus Law is essential for JEE Main candidates, as it forms the basis for solving problems related to light polarization and optics, contributing to a comprehensive understanding of physics concepts.
JEE Main 2025 Subject-Wise Important Chapters
The JEE Main 2025 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.
Check Other Important Links for JEE Main 2025
Prepare effectively for JEE with our comprehensive study material links, including notes, question papers, sample papers, and mock test series for both JEE Main and Advanced. Access essential resources like formulas, important questions, and preparation tips to build your performance.
FAQs on Malus Law for JEE Main 2025
1. What is Analyser in Malus Law?
When light falls on a polarizer, it gets polarized. When this polarized light falls on another Polaroid (an analyzer), it transmits light as per the orientation of its axis with the polarizer.
The light’s intensity transmitted through the analyzer is given by Malus' law.
2. State the Difference Between Unpolarized Light and Plane-Polarized Light.
The difference between unpolarized light and plane-polarized light is as follows.
The electric and magnetic field of a polarized light oscillates in one direction, but the electric field oscillates in all directions in unpolarized light.
Polarized light is coherent, unpolarized light is incoherent.
The Intensity of polarized light depends on the polarizer, and the intensity of unpolarized light depends on the source.
3. Unpolarized Light Passes through Two Successive Polaroids (P1 and P2) the Polaroid P1 Makes Angle θ with the Axis of the Polaroid P2. Find Out the Intensity of the Final Coming Light? And if θ is Varied from 0 to 27, Plot the Intensity Variation Graph?
An unpolarized light passes through two successive polaroids.
We know that when polarized light passes through a polaroid, the intensity of light becomes one-half of the original. If the light is further passed through the polaroids, then its intensity is given by Malus' law
I = 1/2cos2θ
Where,
θ = angle between the axis of the polaroids. Intensity varies from 0 to 2π.
4. How Do You Measure Light Intensity?
To measure the intensity of light first, you have to measure the distance between the source of light and the point. Convert the distance into S.I. units.
For example, if the point of application is at a distance of 56 cm from the source of light, the unit should be 0.56 m.
5. What is the Importance of Polarization in the Concept of Malus Law?
A polarizer signifies a kind of filter that lets the waves of light that are of specific polarization conduct through the filter while blocking the waves of the lights that are of other polarizations. A polarizer is an optical filter that has the capacity of identifying the polarization of the light waves and, depending on that, allows the light wave with a specific polarization to pass through it. It successfully does so by blocking The other light waves that are of specific polarization.
It is especially efficient to filter the light waves that are of undefined polarization or mixed polarization and transform the beam of light into a beam of light that is of well-defined polarization. Since the law of Malus helps students to establish the relationship between the intensity of plane polarised light an analyzer and a polariser, understanding the concept of the polarizer and how the optical filter helps the light waves of a particular polarization pass through the filter is extremely important.
6. What are the Practical Applications of Polarizer?
To understand the concept of how a camera lens works you must have a good understanding of the concept of a polariser. A polarizer works as an optical filter that lets the light waves of a particular polarization pass through the filter and at the same time it blocks the other light waves that are not of the same polarization.
The concept of the polarizer and the usages can be better understood with the help of a camera and the work process of the camera lens. In case you want to click a picture at a very bright place and you want to reduce the exposure or the brightness of the ambience, then a polarizer can help you in doing that. The proper functioning of a polarizer can reduce the quantity of light that enters the lens of the camera and hence it can help you to reduce the brightness of the ambiance as well.
But there are also some limitations with using the polarizer. The polarisers will not help you to click a brilliant shot if you are clicking a picture where there is bright sunlight available. Depending on the layers of the glass of your camera lens, using polarisers can create unnecessary flares. Also, you cannot click a good shot in a dark place or at a place where sunlight is not available. This is because the work of the polarizer is to filter particular waves of light with a specific polarization while blocking the other light waves with other polarizations. If there is no significant amount of light available at a place, then there is no point in filtering a particular light wave as well.
7. What is the Basic Difference between Polarizer and Analyser and their Mechanism?
Polarisers are specific devices that can convert white light whereas Analysers are sort of devices that are used to determine the characteristics of a particular light. Polarisers can convert white lights into plane-polarised lights but Analysers can only determine if a particular light is plane-polarized or not. Since polarisers can convert the white light, that is why they can convert the light beam into a plane-polarized beam of light as well. Analysers can only detect the characteristics of a particular type of light and hence they can only be used in detection.
There are also some differences in the usages of polarisers and Analysers and the positions in which they have to be placed. Polarisers are generally placed under the specimen whereas Analysers are always placed above the specimen. Polarisers can rotate completely and hence they can easily rotate at 360 degrees angle.
The analysers cannot rotate as they can only move according to the path of the light. Polarisers are used to convert the light waves that are coming from a particular light source. Analysers are used to determine the characteristics of the light and to determine whether the light is polarized or not. Analysers are used to determine the polarization of the light to determine the characteristics of the specimen and to conclude if the specimen has the optical properties of refractive index. Analysers are used to do so because the refractive index of a particular specimen depends on the polarisation of light.
8. What are the study materials that I should consult in order to understand the concept of Malus law?
The detailed study guide is now available on the website of Vedantu with the in-depth elaboration of various concepts of physics. The Malus law is especially important for the students of class 12 as it will help them to have the foundational knowledge of the characteristics of light waves and the mechanism of an optical system. All the course materials are formatted in PDF versions.
9. How does the intensity of light change when it passes through a polarizer?
When unpolarized light passes through a polarizer, the intensity of the transmitted light is reduced to half of the initial intensity, regardless of the polarizer's orientation. The intensity after passing through the polarizer is given by $I = \frac{I_0}{2}$.
10. What happens to the intensity of light when it passes through two polarisers with an angle between them?
When light passes through two polarisers, the intensity is reduced according to Malus' Law. If the angle between the axes of the two polarisers is θ\thetaθ, the transmitted intensity III is given by $I = \frac{I_0}{2} \cos^2(\theta)$, where $I_0$ is the initial intensity of the light.
11. What is the role of the angle $\theta$ in Malus' Law?
The angle $\theta$ in Malus' Law represents the angle between the light's polarization direction and the axis of the polarizer. As the angle increases, the transmitted intensity decreases. When $\theta = 90^\circ$, no light is transmitted.
12. Can Malus' Law be applied to light that is already polarized?
Yes, Malus' Law can be applied to already polarized light. The transmitted intensity is still dependent on the angle between the light's polarization direction and the axis of the polarizer, even if the light is initially polarized.
13. How does Malus' Law relate to the concept of electromagnetic waves?
Malus' Law demonstrates the transverse nature of electromagnetic waves, as the intensity of polarized light is related to the alignment of its electric field vector with the polarizer’s axis. The law shows how light, as an electromagnetic wave, behaves when subjected to polarization.
14. How do polarisers and analysers work in a laboratory setup?
In a laboratory setup, polarisers are used to generate plane-polarized light from unpolarized light. Analysers are used to detect and measure the polarization of the transmitted light, providing insight into the light's properties or the characteristics of the sample being studied.
15. What is the significance of Malus' Law in optical communication systems?
Malus' Law plays a role in optical communication systems where polarized light is used for data transmission. The law helps in understanding how the intensity of the signal varies with the alignment of polarisers in the system, ensuring efficient signal transmission and reception.
