




Key Formulas and Examples for Moment of Force in Circular Motion
The concepts of moment of force and circular motion are important in classical mechanics, especially for analyzing the rotational movement of rigid bodies. Understanding the relationship between applied force, rotational axis, and resulting motion is essential for problem-solving in Physics, particularly for exams such as JEE Main.
Rigid Body and Its Characteristics
A rigid body is defined as an idealized solid whose size and shape remain unchanged under the action of external forces. In practical scenarios, bodies that undergo negligible deformation are considered rigid for analytical convenience.
In a rigid body, the distance between any two points remains constant despite applied forces. Such properties are essential when studying both translational and rotational motion in mechanics.
Definition of Moment of Force
The moment of force, also referred to as torque, is the turning effect produced when a force acts on a body at a distance from a fixed axis or point. It is given by the product of the force magnitude and the perpendicular distance between the axis of rotation and the line of action of the force.
The vector form of moment of force is expressed as $\vec{M} = \vec{r} \times \vec{F}$, where $\vec{r}$ is the position vector from the axis to the point of force application, and $\vec{F}$ is the force vector.
Axis of Rotation and Circular Motion
For a rigid body, circular motion occurs when parts of the body move along circular paths about a fixed axis, known as the axis of rotation. Particles located on the axis remain stationary, while others trace circles around the axis.
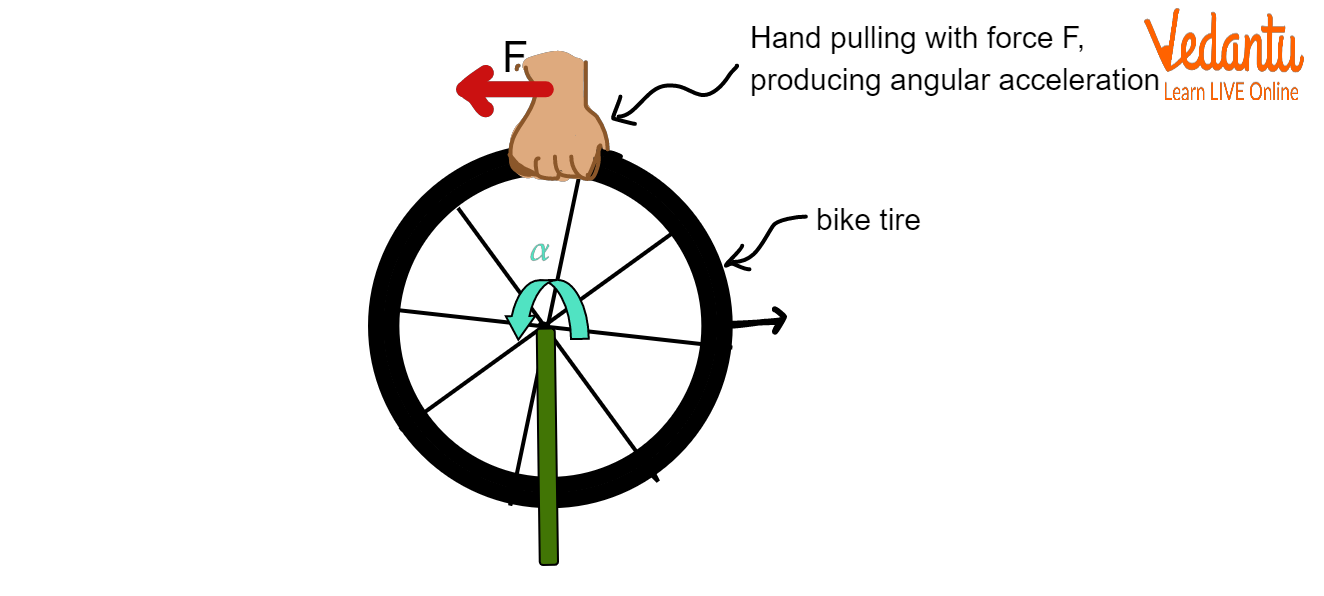
When a force acts on a body hinged at a point, and the force is applied at a distance from the pivot, the body rotates about the axis passing through the pivot due to the generated moment of force.
The study of circular motion includes concepts such as angular velocity, angular acceleration, and the relationship between force, torque, and circular paths. For details, refer to the topic Circular Motion.
Mathematical Expression for Moment of Force
The magnitude of the moment of force is calculated as $M = F \times d$, where $F$ is the magnitude of the force and $d$ is the perpendicular distance (moment arm) from the axis of rotation to the line of action of the force.
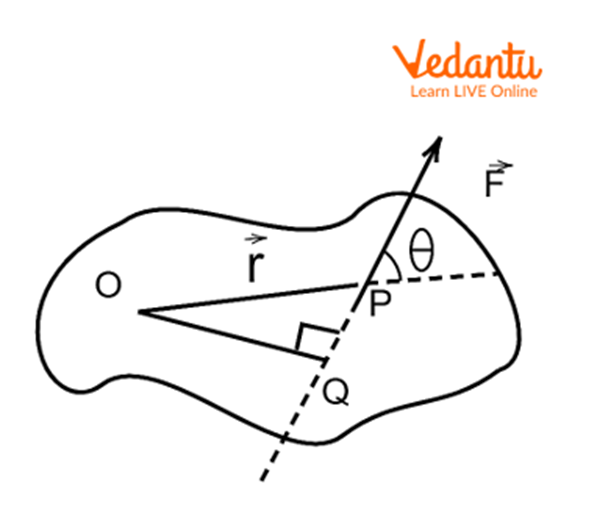
If the force $\vec{F}$ is applied at a point with position vector $\vec{r}$ at an angle $\theta$ to $\vec{r}$, then magnitude of the moment is $M = F r \sin \theta$.
The direction of torque or moment of force is given by the right-hand thumb rule and is perpendicular to the plane containing $\vec{r}$ and $\vec{F}$.
SI Unit and Dimensions of Moment of Force
The SI unit of moment of force is newton-metre ($\text{N}\cdot \text{m}$). It is a vector quantity having dimensions $[M^1L^2T^{-2}]$.
Derivation of Moment of Force Formula
Consider a body capable of rotating about a fixed axis passing through point $O$. A force $\vec{F}$ is applied at point $P$ such that the position vector from $O$ to $P$ is $\vec{r}$, and the angle between $\vec{F}$ and $\vec{r}$ is $\theta$.
The perpendicular distance, or moment arm, is $r \sin \theta$. Thus, the moment of force is $M = F \cdot r \sin \theta$. In vector form: $\vec{M} = \vec{r} \times \vec{F}$.
Factors Influencing Moment of Force
The magnitude of the moment of force depends linearly on the force applied and the length of the moment arm from the axis of rotation. Increasing either factor increases the torque produced.
- Magnitude of applied force
- Length of moment arm
- Angle between force and position vector
These concepts are essential for understanding devices such as levers and spanners, as well as practical applications like opening doors or rotating machinery. The mechanical advantage achieved by increasing the moment arm is a fundamental principle in Physics.
Distinction Between Force and Moment of Force
A force acting on the centre of mass of a body results in linear acceleration, while a force applied at a distance from the axis of rotation creates a turning effect, producing angular acceleration about the axis.
| Force | Moment of Force (Torque) |
|---|---|
| Produces linear acceleration | Produces angular acceleration |
| SI unit: newton (N) | SI unit: newton-metre (N·m) |
| Acts at any point | Depends on point of application |
| $F = m \times a$ | $M = I \times \alpha$ |
The concept of moment of inertia is significant for analyzing rotational dynamics, as it measures a body's resistance to angular acceleration under the action of torque. To study further, visit Moment Of Inertia.
Applications and Examples of Moment of Force
The principles of moment of force are fundamental in everyday mechanisms. Using a longer lever arm to lift heavy objects, applying force at the free end of a door, and turning a tight nut with a spanner are direct applications of torque concepts.
- Efficient lifting using levers
- Easy door operation at the free end
- Spanners for loosening or tightening nuts
Analysis of such systems also often includes frictional effects. For comprehensive discussion, refer to Static And Dynamic Friction.
Relation to Work, Energy and Stationary Waves
When a torque acts and a body rotates through an angle, work is done, and the energy associated with this rotation is linked to both angular displacement and moment of inertia. The distinction between such physical quantities is explored in Difference Between Work And Energy.
The study of rotational dynamics and oscillatory systems, such as stationary waves, involves understanding torque-induced angular motion and its energy transformations. A detailed analysis of oscillatory behavior can be found in Stationary Waves.
Summary
The moment of force provides a quantitative measure of the turning effect produced by a force applied at a distance from an axis. It is essential for analyzing both static and dynamic equilibrium in rotational mechanics, forming the basis of torque-based questions in competitive examinations.
FAQs on Understanding Moment of Force and Circular Motion
1. What is the moment of force in physics?
Moment of force (also called torque) is the turning effect produced when a force is applied at a distance from a pivot point or axis of rotation.
Key points about moment of force:
- Calculated as the product of force and perpendicular distance from the pivot (Moment = Force × Distance)
- Measured in Newton-metre (N·m)
- Direction is given by the right-hand rule
- Crucial in understanding rotation in circular motion and mechanics
2. State the conditions necessary for achieving equilibrium of moments.
Equilibrium of moments is achieved when the total clockwise moments equal the total anticlockwise moments about the same axis.
Conditions include:
- The sum of clockwise moments = sum of anticlockwise moments
- No net turning effect is present—body remains at rest or in uniform rotation
- Both translational and rotational equilibrium must be considered
3. Define circular motion and give two examples.
Circular motion is the movement of an object along a circular path at a constant distance from a fixed point.
Examples include:
- The revolution of planets around the Sun
- The rotation of a ceiling fan blade
4. What is the difference between centripetal and centrifugal force in circular motion?
Centripetal force is the force that keeps a body moving in a circular path directed towards the center of the circle, while centrifugal force is an apparent force directed away from the center, experienced in a rotating reference frame.
Differences:
- Centripetal force is real and necessary for circular motion
- Centrifugal force is a pseudo-force observed from the rotating body’s frame
5. How is torque related to rotational motion?
In rotational motion, torque (moment of force) determines the rate at which an object’s angular velocity changes.
Key points:
- A greater torque means greater angular acceleration
- Given by Torque = Force × Perpendicular Distance from pivot
- Essential for starting, stopping, or changing rotational motion
6. State the principle of moments with an example.
The principle of moments states that for a body in equilibrium, the sum of clockwise moments about any point equals the sum of anticlockwise moments about that point.
Example:
- A seesaw balances when a heavier child sits closer to the fulcrum and a lighter child sits farther, so their moments are equal and opposite.
7. What factors affect the magnitude of the moment of force?
The magnitude of the moment of force depends on:
- The amount of force applied
- The perpendicular distance from the axis or pivot point
- Angle at which the force is applied—the maximum moment is when force is perpendicular to the arm
8. Why is centripetal force necessary for circular motion?
A centripetal force is essential to keep any object moving in a circular path, as it continuously pulls the object towards the center.
Without this force:
- The object would move off in a straight line due to inertia (Newton's first law)
- Circular motion would not be possible
9. Write the mathematical expression for moment of force and state its SI unit.
Mathematical expression: Moment of Force (Torque), τ = Force (F) × Perpendicular distance (r) from the axis of rotation.
SI unit: Newton-metre (N·m)
10. What is meant by uniform circular motion?
Uniform circular motion refers to the motion of an object moving along a circular path with a constant speed.
Key points:
- Only speed (not velocity) remains constant
- Direction of motion changes continuously
- Requires constant centripetal force
11. What is the SI unit of moment of force?
The SI unit of moment of force (torque) is Newton-metre (N·m).
12. Why does a door open easier when force is applied at its edge rather than near the hinge?
A door opens more easily when force is applied at the edge because the moment of force increases with the distance from the hinge (pivot point).
Key points:
- Greater distance = greater moment for the same force
- This makes rotation about the hinge easier and more efficient
























