




Formula to Find the Number of Images Between Two Mirrors
The number of images formed by two plane mirrors depends on the angle between the mirrors and the position of the object. This principle is widely applied in optics to understand the behavior of reflected rays and the formation of multiple images. Such understanding is essential for solving related problems in the JEE Main syllabus.
Plane Mirrors and Their Reflective Properties
A plane mirror is a flat, polished reflective surface usually coated with silver or aluminium. When light rays strike the surface, they reflect according to the laws of reflection, resulting in the formation of virtual and erect images. The image formed by a single plane mirror is always of the same size as the object and is laterally inverted. To learn more about these fundamental principles, refer to Difference Between Reflection And Refraction.
Images Formed by Two Plane Mirrors
When two plane mirrors are inclined to each other at a certain angle, the number of images increases due to successive reflections between the mirrors. This number depends on the inclination angle and the symmetry of the object's placement with respect to the mirrors.

Formula for Number of Images Formed
The standard formula to calculate the number of images ($n$) formed by two plane mirrors inclined at an angle $\theta$ is:
$n = \dfrac{360}{\theta} - 1$
Here, $\theta$ is the angle between the mirrors in degrees. If $\dfrac{360}{\theta}$ is not an integer, only the integer part is considered for the number of images when the object is placed asymmetrically.
Number of Images: Special Cases and Interpretation
When the value of $\dfrac{360}{\theta}$ is an integer and the object is placed symmetrically between the mirrors, the number of images is $(\dfrac{360}{\theta} - 1)$. For asymmetrical placement and non-integer results, the number of images corresponds to the integer part of $\dfrac{360}{\theta}$.
If the mirrors are placed parallel to each other ($\theta = 0^\circ$), the number of images becomes theoretically infinite due to repeated reflections. Perpendicular placement ($\theta = 90^\circ$) yields three images. Additional details regarding lateral displacement and related phenomena are discussed at Lateral Displacement Of Light.
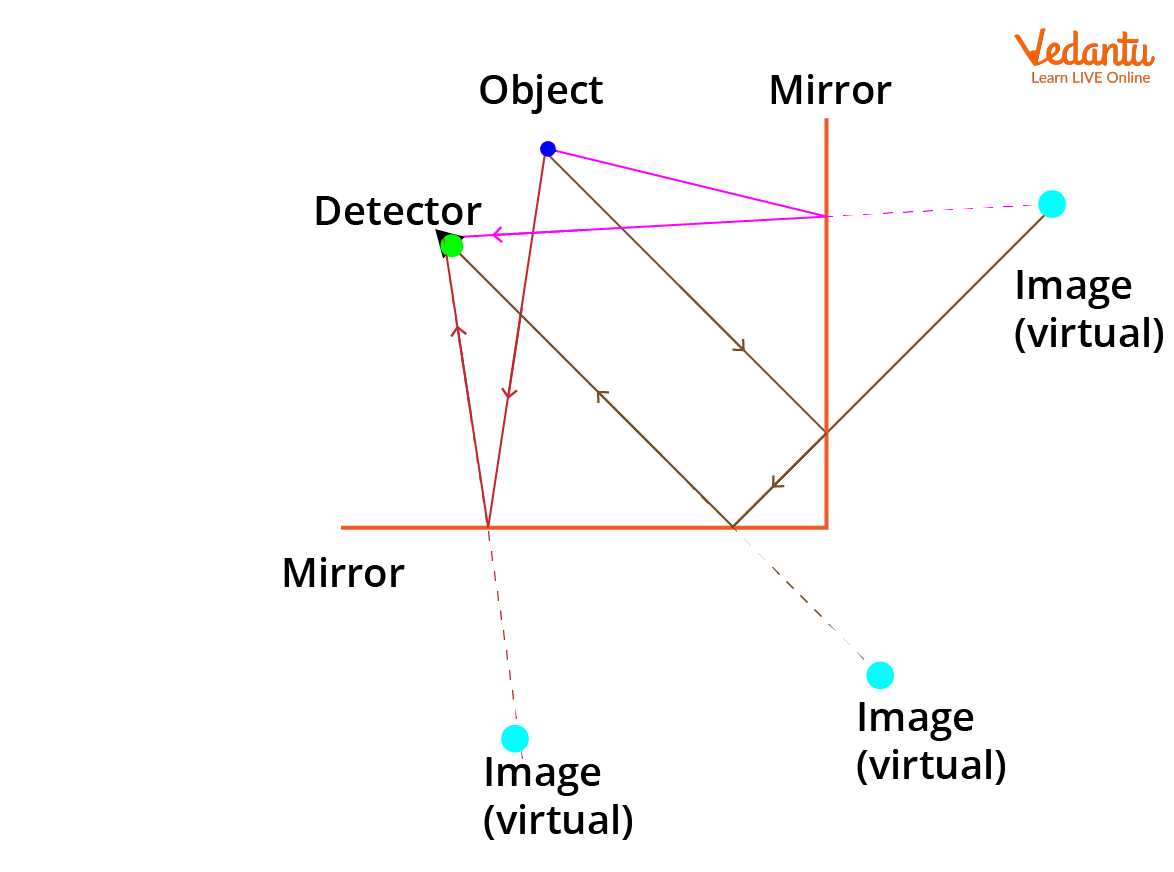
Example Calculations of Number of Images
For two plane mirrors at $60^\circ$, the number of images is calculated as $n = \dfrac{360}{60} - 1 = 5$. For an angle of $72^\circ$, $n = \dfrac{360}{72} = 5$, thus five images are formed for unsymmetrical placement. For an angle of $45^\circ$, the formula gives $n = \dfrac{360}{45} - 1 = 7$.
| Angle Between Mirrors ($\theta$) | Number of Images ($n$) |
|---|---|
| $60^\circ$ | 5 |
| $72^\circ$ | 5 |
| $90^\circ$ | 3 |
| $45^\circ$ | 7 |
Factors Affecting the Number of Images
The number of images is affected by the angle between the mirrors and the object’s position. Symmetrical placement may increase the number of images by one when $\dfrac{360}{\theta}$ is an integer. For non-integer results, only the integer part is considered for asymmetrical placement.
Other aspects such as the type of mirror, orientation, and laws of reflection also influence the overall image formation. To explore additional optics concepts, refer to Sign Convention Of Lens And Mirror.
Applications and Examples
This principle of image formation by inclined plane mirrors is used in devices like kaleidoscopes and periscopes. Understanding the number of images is important in various scientific applications and problem-solving in physics. Applications further relate to principles of magnification, which are explained at Mirror Formula And Magnification.
Key Points on Number of Images Formed
- The number decreases as the angle increases
- Parallel mirrors create theoretically infinite images
- Object position (symmetrical/asymmetrical) matters
- Odd and even values of $\dfrac{360}{\theta}$ affect result
Summary Table and Further Study
The systematic use of the formula directly relates to questions commonly encountered in competitive exams. A clear understanding aids in analyzing ray diagrams and predicting outcomes in multiple-mirror systems. For further related topics, one can study the Principle Of Superposition Of Waves and other fundamental properties discussed in optics.
FAQs on How Many Images Are Formed by Two Plane Mirrors?
1. How many images are formed by two plane mirrors placed at a certain angle?
When two plane mirrors are placed at an angle θ, the number of images formed is calculated using the formula: N = (360/θ) - 1 (if 360°/θ is not an integer); if it is an integer, then N = (360/θ) - 1 or N = 360/θ - 1. In summary, the number of images depends on the angle between the mirrors:
- If θ = 90°, then N = 3 images
- If θ = 60°, then N = 5 images
- If θ = 45°, then N = 7 images
- If mirrors are parallel (θ = 0°), images are infinite
2. What is the formula to calculate the number of images formed by two plane mirrors?
The number of images (N) formed by two plane mirrors placed at an angle θ can be determined using the formula:
- N = (360°/θ) - 1 if 360°/θ is not an integer
- N = (360°/θ) - 1 or N = 360°/θ - 1 if 360°/θ is an integer and object is not placed symmetrically
This formula uses angle between mirrors and applies to CBSE physics and science syllabi for classes 8–10.
3. Why does the number of images increase when the angle between two mirrors decreases?
The number of images increases because a smaller angle (θ) between the two plane mirrors allows more reflections. This happens due to:
- Multiple reflections occurring as light bounces between the mirrors
- Decreasing angle means more opportunities for rays to reflect, creating more images
- As angle approaches zero, the number of images approaches infinity
4. What happens to the number of images if two plane mirrors are at right angles?
When two plane mirrors are placed at a right angle (90°), exactly 3 images of an object are formed. This is because the formula N = (360/90) - 1 = 3 applies. This setup is commonly used in periscopes and kaleidoscopes.
5. Can the number of images formed by two plane mirrors ever be infinite?
Yes, if two plane mirrors are placed parallel to each other (angle θ = 0°), the number of images becomes infinite. The light keeps reflecting back and forth indefinitely. This principle is used in some optical devices to demonstrate infinite reflections.
6. What are some examples where multiple images by plane mirrors are seen in daily life?
Multiple images from plane mirrors are commonly observed in:
- Kaleidoscopes – show symmetrical patterns by using angled mirrors
- Barber shops – mirrors opposite each other create many images
- Periscopes – use right-angled mirrors for seeing above obstacles
7. Do object position or placement affect the number of images formed by plane mirrors?
For two plane mirrors, position can affect the number of images only when the object is placed symmetrically (exactly on the angle bisector). If not centrally placed, the formula N = (360/θ) - 1 is used; however, symmetry may create some overlapping or missing images in special cases.
8. Explain with reason: If two plane mirrors are placed at an angle of 60°, how many images will be formed?
At θ = 60°, use the formula: N = (360/60) - 1 = 6 - 1 = 5 images. Placing mirrors at 60° allows for five images due to repeated reflections according to the geometry.
9. Is there any exception where the expected number of images is not formed?
Yes, exceptions occur if the object is placed on the angle bisector when 360°/θ is an even integer. In such symmetry, some images may overlap, leading to fewer images than calculated. This is important in exam answers for CBSE physics.
10. How does the number of images formed change with increasing angle between plane mirrors?
As the angle between plane mirrors increases, the number of images decreases because the formula N = (360/θ) - 1 gives smaller N for larger θ. For example:
- If θ = 120°, N = 360/120 - 1 = 2 images
- If θ = 180°, N = 360/180 - 1 = 1 image
























