




Step-by-Step Path and Effects of Light Passing Through a Prism
The path of a ray of light through a prism illustrates the principles of refraction, deviation, and dispersion. When light passes through a glass prism, its direction changes due to differences in the refractive indices of air and glass. This phenomenon is essential for understanding various optical effects and is fundamental in physics education, especially in the context of the JEE Main examination.
Structure and Properties of a Prism
A prism is a transparent optical element with two non-parallel, flat refracting surfaces inclined at a specific angle called the angle of the prism. Typically, a triangular glass prism is used in laboratory experiments to study the refraction and deviation of light. The refracting angle is commonly 60° for an equilateral prism.
The basic geometry and construction of a prism make it suitable for bending, splitting, or deviating light rays. For an in-depth discussion of prism types and their applications, refer to Understanding Prisms.
Refraction of Light Through a Prism
When a light ray enters the prism from air, it travels from a rarer medium (air) into a denser medium (glass). This causes the ray to bend towards the normal at the first refracting surface. As it exits the prism into air, it moves from a denser medium to a rarer medium and bends away from the normal. The combined effect results in the overall deviation of the ray from its original path.
The path inside the prism is governed by Snell’s law, which relates the angle of incidence, angle of refraction, and the refractive indices of the two media. The law is mathematically expressed as $n_1 \sin i = n_2 \sin r$, where $i$ and $r$ are the angles of incidence and refraction, respectively.
A detailed explanation of this concept is available at Refraction of Light Through Prism.
Stepwise Tracing of the Path of Ray of Light Through a Glass Prism
The standard practical procedure for tracing the path of a ray of light through a glass prism is as follows. First, place the prism on a white sheet of paper and mark its outline. Draw a normal to one face at a chosen point, and draw the incident ray at a specific angle to this normal. Insert pins along this incident ray. Then, from the other side of the prism, align another set of pins such that they appear collinear with the first set when viewed through the prism. Connect the pin points to trace the refracted and emergent rays, and extend them to intersect the prism’s outline.
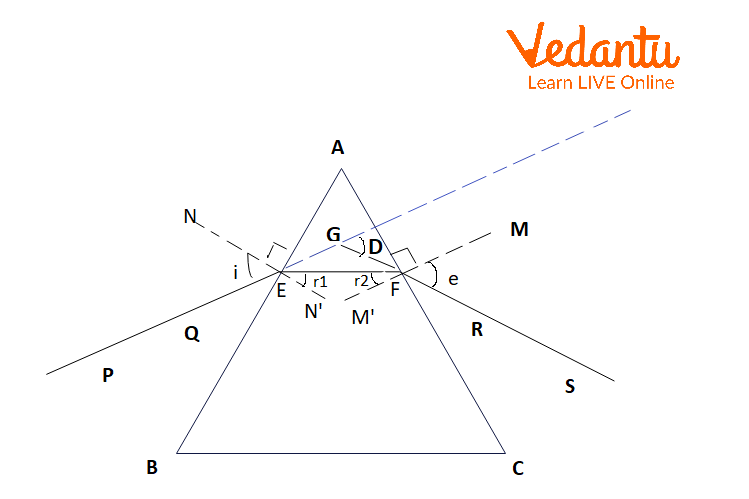
The diagram illustrates the incident ray entering the prism, refracted ray inside the prism, and the emergent ray exiting at the second refracting surface. Angles such as the angle of incidence, angle of refraction, angle of emergence, and angle of deviation are clearly marked.
Angle of Deviation and Related Angles
The angle of deviation ($D$) is the angle between the direction of the incident ray and the direction of the emergent ray, when extended to meet at a point. The following angles are involved in the experiment:
- Angle of incidence ($i_1$): between incident ray and normal
- Angle of refraction ($r_1$): between refracted ray and normal inside prism
- Angle of emergence ($i_2$): between emergent ray and normal at exit surface
- Angle of prism ($A$): between prism surfaces
The relationship between these angles is given by the equation $D = i_1 + i_2 - A$. At minimum deviation, the equation for refractive index ($\mu$) becomes $\mu = \dfrac{\sin \left(\dfrac{A+D_m}{2}\right)}{\sin \left(\dfrac{A}{2}\right)}$, where $D_m$ is the minimum angle of deviation.
Dispersion of Light by a Prism
A glass prism can also split white light into its constituent colors, a process known as dispersion. Each color has a different wavelength and thus experiences a different refractive index in the medium. This results in varied deviation angles, producing a spectrum of colors from violet (which bends most) to red (which bends least).
Experimental Observations: Path of Ray in Glass Prism
Key observations made during the tracing of the ray through a glass prism include the following. The incident ray bends towards the normal at the first surface, travels through the prism, and bends away from the normal at the second surface. The net result is a deviation of the emergent ray towards the base of the prism.
| Angle | Description |
|---|---|
| Angle of Incidence ($i_1$) | Between incident ray and normal |
| Angle of Emergence ($i_2$) | Between emergent ray and normal |
| Angle of Prism ($A$) | Between prism surfaces |
| Angle of Deviation ($D$) | Between incident and emergent ray |
Factors Affecting the Path of Light through a Prism
Several factors affect the deviation and dispersion of light in a prism. These include the angle of incidence, the angle of the prism, and the material’s refractive index. The wavelength of light also plays a significant role, as different wavelengths travel at different speeds in glass.
Sign conventions used in prism-related problems are essential and can be further studied in Sign Convention in Optics.
Mathematical Expression for Deviation
The formula for the refractive index ($\mu$) in terms of the prism angle ($A$) and the minimum deviation ($D_m$) is: $\mu = \dfrac{\sin \left(\dfrac{A + D_m}{2}\right)}{\sin \left(\dfrac{A}{2}\right)}$. This relation is crucial for numerical calculations in prism-based problems at the JEE Main level.
Applications and Use of Prisms
Prisms are widely used in spectrometers, periscopes, binoculars, and other optical instruments to deviate and analyze light. Their property of dispersing white light into constituent colors is fundamental in spectroscopy and optical studies.
Detailed notes on optics and related topics are available at Optics Revision Notes.
FAQs on How Does Light Travel Through a Prism?
1. What is the path of a ray of light through a prism?
The path of a ray of light through a prism involves refraction at two surfaces, causing the light to bend and deviate from its original direction.
Here are the steps:
- The light enters the prism and bends towards the normal at the first surface (refraction).
- Inside the prism, the ray travels in a straight line but at a new angle.
- When exiting, the ray bends away from the normal at the second surface (second refraction).
- The final direction of the emergent ray is deviated from its original path.
2. Why does a ray of light deviate when passing through a prism?
A ray of light deviates through a prism because of refraction at its two non-parallel surfaces.
Key points include:
- The light changes speed and direction due to the difference in optical density between air and glass.
- Each surface bends the ray differently, resulting in the overall deviation of the incident ray.
- This deviation depends on the angle of prism, type of material, and the wavelength of light.
3. What is meant by angle of deviation in a prism?
The angle of deviation is the angle between the direction of the incident ray and the emergent ray after passing through the prism.
Some important points:
- It measures the extent a ray is bent by the prism.
- A smaller angle of incidence can sometimes result in a minimum deviation.
- This angle is used to calculate the refractive index of the prism material.
4. What happens to white light when it passes through a glass prism?
When white light passes through a glass prism, it splits into its constituent colors, a phenomenon called dispersion.
Main points:
- Each color bends at a different angle due to different wavelengths.
- This forms a spectrum ranging from violet to red.
- A prism thus demonstrates that white light is made up of various colors.
5. How do you represent the path of a light ray through a prism diagrammatically?
The path of a light ray through a prism is represented by a labeled ray diagram.
Main features include:
- Incident ray: enters the prism and bends towards the normal.
- Refracted ray: travels within the prism.
- Emergent ray: exits, bending away from the normal.
- Key angles: angle of incidence (i), angle of refraction (r), angle of emergence (e), and angle of deviation (D).
6. Why does the emergent ray bend away from the base of the prism?
The emergent ray bends away from the base of a prism due to refraction, as light passes from a denser medium (glass) to a rarer medium (air) at the prism's second face.
This causes the ray to deviate away from the base, in accordance with the laws of refraction.
7. What is minimum deviation?
Minimum deviation occurs when the path of the ray inside the prism is parallel to the base, and the angle of deviation is at its lowest.
Key facts:
- The emergent and incident rays are equally inclined to the prism faces.
- This concept helps in finding the refractive index of prism materials.
8. What are the practical applications of prisms in optics?
Prisms have several applications in optics due to their ability to bend, reflect, or split light.
Main uses:
- Spectroscopy – analyzing light spectra.
- Periscopes and binoculars – changing light direction.
- Camera viewfinders – image correction.
- Optical instruments for scientific research.
9. State the laws of refraction as applied to a ray passing through a prism.
The laws of refraction (Snell's law) state how the light ray bends at each surface of the prism.
Key points:
- The incident ray bends towards the normal when entering the denser medium (glass).
- The emergent ray bends away from the normal when leaving to the rarer medium (air).
- The ratio of the sine of the angle of incidence to the sine of the angle of refraction is constant for given media.
10. What is the relation between refractive index, angle of prism, and angle of minimum deviation?
The refractive index (μ) of prism material can be derived using the angle of the prism (A) and angle of minimum deviation (Dmin).
The formula is:
- μ = sin((A + Dmin)/2) / sin(A/2)
























