Series And Parallel Combination Of Spring for JEE Main Physics 2025

When multiple springs are connected, they can be arranged in two main configurations: series and parallel. The behaviour of the system changes depending on how the springs are combined. Understanding the series and parallel combination of springs is important in physics for JEE Main Exam, as it helps determine the overall spring constant, force, and extension or compression of the system.

In a series combination, the springs are connected end-to-end, and the total extension or compression is the sum of the individual extensions. In contrast, in a parallel combination, the springs are connected side-by-side, and the total force is the sum of the forces exerted by each spring.

Series Combination of Springs

Suppose we have a block attached to a system of springs in series combination as shown in the diagram below.

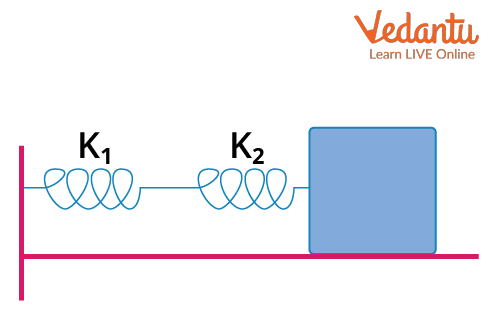
Two Springs in Series Combination

The spring constants of the springs are k1 and k2, and they are connected in series.

Suppose we apply a force on the combination of springs through the block. The force on both the springs will be the same. However, the displacement of each spring might be different.

If the spring having spring constant k1 is displaced by x1 and similarly the spring having spring constant k2 is displaced by x2, then the total displacement of both springs can be written as

x = x1 + x2

We know that for spring 

F = -kx

Using this we can write

$\begin{align} &-\dfrac{F}{k}=\left(\dfrac{-F}{k_{1}}\right)+\left(\dfrac{-F}{k_{2}}\right) \\ &-\dfrac{F}{k}=-F\left(\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}\right) \\ &\dfrac{1}{k}=\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}} \end{align}$

Here, k is the equivalent spring constant of the combination.

Now we know that 

$\begin{align} &\omega^{2} x=k \\ &\omega=\sqrt{\dfrac{k}{x}} \end{align}$

We also know that the time period can be written as

$T=\dfrac{2 \pi}{\omega}$

Combining the equations, we can write

$T=2 \pi \sqrt{\dfrac{m}{k}}$ ....(1)

This time period is also known as the springtime. 

Inserting the value of k for the series combination, we get

$T=2 \pi \sqrt{m\left(\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}\right)}$

This is the time period of the combination.

The formula for the equivalent spring constant can be extended to a system of n springs in a series combination. We can write

$\dfrac{1}{k}=\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}+\ldots+\dfrac{1}{k_{n}}$

Key Points on Series Combination of Spring:

• The total extension of the system is the sum of the extensions of the individual springs.

• The force acting on each spring is the same.

Spring in Series Formula:

For springs with spring constants $k_1, k_2, k_3, \dots$ the total spring constant $k_{\text{total}}$ for the system in series is given by:

$\dfrac{1}{k_{\text{total}}} = \dfrac{1}{k_1} + \dfrac{1}{k_2} + \dfrac{1}{k_3} + \dots$

Where:

• $k_{\text{total}}$​ is the effective spring constant for the series combination.

• $k_1, k_2, k_3, \dots$are the spring constants of the individual springs.

Since the total spring constant decreases in a series combination, the overall stiffness of the system is reduced.

Series Combination of Springs Example:

If two springs, one with a spring constant of $100 \, \text{N/m}$ and another with$200 \, \text{N/m}$, are connected in series, the total spring constant $k_{\text{total}}$​ is:

$\dfrac{1}{k_{\text{total}}} = \dfrac{1}{100} + \dfrac{1}{200} = \dfrac{3}{200}$

$k_{\text{total}} = \dfrac{200}{3} \approx 66.67 \, \text{N/m}$

Parallel Combination of Springs

Suppose we now have a combination of springs in parallel as shown in the figure below.

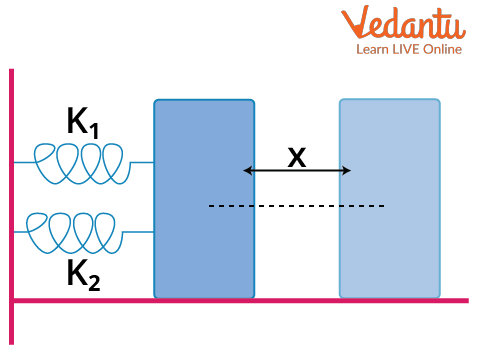
Two Springs in a Parallel Combination

The spring constants are k1 and k2. As it is visible in the figure, the springs are connected in parallel to a block. Let’s suppose that we displace the block by a distance x. The displacement of both the blocks, in this case, will be the same, but the force by each spring will be different. However, we can write the sum of the forces of the combination F as: 

F =F1 + F2

Using the equation of SHM, we can write

$\begin{align} &-k x=-k_{1} x+\left(-k_{2} x\right) \\ &-k x=-x\left(k_{1}+k_{2}\right) \\ &k=k_{1}+k_{2} \end{align}$

This is the equivalent spring constant of the springs in a parallel combination. 

The time period of this combination can be found by substituting the value of the equivalent spring constant in equation (1). This gives

$\begin{align} &T=2 \pi \sqrt{\dfrac{m}{k}} \\ &T=2 \pi \sqrt{\dfrac{m}{k_{1}+k_{2}}} \end{align}$

We can also generalise the formula for the equivalent spring constant for a combination of n springs in a parallel combination. The equivalent spring constant will then be

$k_{p}=k_{1}+k_{2}+\ldots+k_{n}$

Key Points on Parallel Combination of Spring

• The total extension (or compression) of the system is the same for all springs.

• The total force acting on the system is the sum of the forces acting on each individual spring.

Formula for Spring Constant in Parallel

For springs with spring constants $k_1, k_2, k_3, \dots$ the total spring constant $k_{\text{total}}$​ for the system in parallel is given by:

$k_{\text{total}} = k_1 + k_2 + k_3 + \dots$

Where:

• $k_{\text{total}}$ is the effective spring constant for the parallel combination.

• $k_1, k_2, k_3, \dots$ are the spring constants of the individual springs.

Since the total spring constant increases in a parallel combination, the overall stiffness of the system is greater.

Example Parallel Combination of Spring

 If two springs, one with a spring constant of $100 \, \text{N/m}$ and another with $200 \, \text{N/m}$, are connected in parallel, the total spring constant $k_{\text{total}}$ is:

$k_{\text{total}} = 100 + 200 = 300 \, \text{N/m}$

Numerical Examples on Series and Parallel Combination of Springs

Example 1: Identical springs of spring constant K are connected in series and parallel combinations. A mass m is suspended from them. Find the ratio of the time periods of their vertical oscillation.

Solution: For series combination, the equivalent spring constant ks will be

$\begin{align} &\dfrac{1}{k_{s}}=\dfrac{1}{k}+\dfrac{1}{k} \\ &\dfrac{1}{k_{s}}=\dfrac{2}{k} \\ &k_{s}=\dfrac{k}{2} \end{align}$

The time period of this combination will be

$T_{s}=2 \pi \sqrt{\dfrac{2 m}{k}}$

Similarly, the equivalent spring constant kp for the parallel combination will be

$\begin{align} &k_{p}=k+k \\ &k_{p}=2 k \end{align}$

The time period of this parallel combination will be

$T_{p}=2 \pi \sqrt{\dfrac{m}{2 k}}$

The ratio of TS and TP  will then be

$\begin{align} &\dfrac{T_{s}}{T_{p}}=\dfrac{2 \pi \sqrt{\dfrac{2 m}{k}}}{2 \pi \sqrt{\dfrac{m}{2 k}}} \\ &\dfrac{T_{s}}{T_{p}}=\sqrt{\dfrac{2 m}{k} \times \dfrac{m}{2 k}} \\ &\dfrac{T_{s}}{T_{p}}=\sqrt{4} \\ &\dfrac{T_{s}}{T_{p}}=2 \end{align}$

The ratio of the time period of the series and the parallel combination is 2:1.

Example 2: The resultant force acting on a particle that is attached to a spring executing simple harmonic motion is 10 N, when it is 2 m away from the centre of oscillation. Find the spring constant.   

Solution: The force by the spring is given as 

F=-kx

Since we need only the magnitude of k, we can ignore the negative sign which shows us the direction of the force. The magnitude of the spring constant can be written as

$\begin{align} &k=\left|\dfrac{F}{x}\right| \\ &k=\left|\dfrac{10}{2}\right| \\ &k=5 \mathrm{Nm}^{-1} \end{align}$

The spring constant of the spring is 5 Nm-1.

Applications of Series and Parallel Combinations of Springs

1. Shock Absorbers:

In vehicles, shock absorbers use a combination of springs to manage forces and dampen the impact. Depending on whether the springs are arranged in series or parallel, the suspension system is designed for optimal performance.

2. Suspension Systems:

For smooth rides, car suspension systems use springs in parallel to distribute forces, ensuring that the vehicle remains balanced and stable while driving on uneven surfaces.

3. Measuring Instruments:

Springs are used in force meters and spring scales to measure force or weight. The configuration of the springs determines the sensitivity and range of measurement.

4. Heavy Equipment:

In large machinery or structural engineering, the correct spring configuration can help distribute weight and reduce the impact of heavy forces, increasing the durability and lifespan of the equipment.

5. Design of Musical Instruments:

Springs in musical instruments like pianos or organs are used to create tension for the strings. The arrangement of springs can affect the pitch and quality of the sound produced.

Conclusion

A particular kind of oscillation in which the particle accelerates along a straight route is known as simple harmonic motion. The unique feature of this motion is that the particle's acceleration is always pointed in the direction of a fixed point, and the strength of the acceleration is inversely proportional to the particle's displacement from the fixed point. The fixed point is referred to as the oscillation's centre. A spring and mass system executes SHM. The restoring force by a spring having spring constant k and displacement x is given as 

F=-kx

The equivalent spring constant of a system of n springs connected in series is given as

$\dfrac{1}{k_{s}}=\dfrac{1}{k_{1}}+\dfrac{1}{k_{2}}+\ldots+\dfrac{1}{k_{n}}$

Similarly, the equivalent spring constant of a system of n springs connected in parallel is given as

$k_{p}=k_{1}+k_{2}+\ldots+k_{n}$

JEE Main 2025 Subject-Wise Important Chapters

The JEE Main 2025 subject-wise important chapters provide a focused strategy for Chemistry, Physics, and Maths. These chapters help students prioritise their preparation, ensuring they cover high-weightage topics for better performance in the exam.

Check Other Important Links for JEE Main 2025

JEE Main and JEE Advanced 2025 needs well-structured study materials. Here are some valuable resources to help you plan your preparation and practice efficiently.