Hooke’s Law: Real-Life Examples and How to Solve Problems
Springs and spring forces play a crucial role in understanding elastic behavior in Physics, especially for JEE and NEET aspirants.
Whenever a spring is compressed or stretched from its natural length, it exerts a force tending to restore its original shape. This force is called the spring force.
Imagine pressing down a spring in a pen; the moment you release, it pushes back and returns the tip upwards. This daily occurrence is governed by a simple yet powerful law.
Springs store mechanical energy when deformed, making them essential for devices like car suspensions and measuring instruments.
Visualizing Spring Force: Compression and Extension
The force a spring exerts depends on how much you compress or stretch it. The farther you push or pull, the more strongly it pushes or pulls back.
Both compression and extension involve the spring force acting opposite to the direction of displacement, ensuring equilibrium can be achieved in systems like spring-mass assemblies.
When studying the Concept of Spring Force, it's important to note that every real-world spring has a limit beyond which it does not return to its shape.
Hooke's Law: The Foundation of Spring Force
Hooke’s Law states that the force exerted by a spring is directly proportional to the displacement from its equilibrium position, provided the deformation stays within the elastic limit.
Mathematically, this is written as $F = -k x$, where $F$ is the restoring force, $k$ is the spring constant, and $x$ is the displacement.
The negative sign indicates that the force acts in the direction opposite to the applied displacement.
You can explore a detailed breakdown in the article on Understanding Hooke's Law for deeper conceptual clarity.
Spring Constant and Stiffness Explained
The spring constant, $k$, measures a spring's stiffness; higher $k$ means you need more force for the same displacement. It is defined as $k = \dfrac{F}{x}$.
The units of $k$ are $\dfrac{N}{m}$, which indicates the force needed to stretch or compress the spring by one meter.
| Parameter | Unit/Definition |
|---|---|
| Spring Force ($F$) | Newton (N) |
| Displacement ($x$) | Meter (m) |
| Spring Constant ($k$) | N/m |
Each application, from weighing machines to car suspensions, relies critically on an accurately chosen value of $k$ for performance and safety.
Further insights on how spring constants affect oscillatory motion are discussed in Spring Block Oscillations.
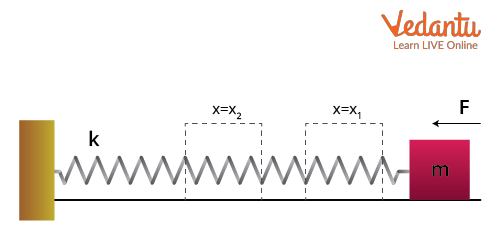
Mathematical Interpretation: Work Done by Spring Force
The work done by a spring force during compression or extension from $x_1$ to $x_2$ is $W = \dfrac{1}{2} k (x_1^2 - x_2^2)$, derived using calculus principles.
The result shows that the work done depends on the change in the square of the displacement, not just the distance moved.
Whenever a spring returns to its original state, the work done appears as mechanical energy, explained further in Elastic Potential Energy Analysis.
Types and Applications of Springs
- Helical springs in vehicle suspensions absorb shocks smoothly
- Compression springs in medical syringes store potential energy
- Tension springs in trampolines provide bounce and resilience
- Torsion springs in door hinges restore angular positions
Each type of spring is designed for a specific role, depending on the need for compression, tension, or rotation.
For a broad overview, see Spring Force Overview covering various real scenarios.
Solved Example: Numerical Problem on Spring Force
A spring with $k = 250\, N/m$ is stretched by $0.08\,m$. The force required is $F = kx = 250 \times 0.08 = 20\,N$. The work done in stretching is $W = \dfrac{1}{2} k x^2 = \dfrac{1}{2} \times 250 \times (0.08)^2 = 0.8\,J$.
Practice Question: Check Your Understanding
If a $60\,N/m$ spring is compressed by $5\,cm$, calculate the magnitude of the restoring force.
Graphical Insight: Force vs. Displacement Curve
A straight line passing through the origin in a $F$ vs $x$ graph shows the linear relationship between force and displacement, as per Hooke's Law.
Non-linear behavior indicates the spring is beyond its elastic limit, and Hooke’s Law no longer applies.
JEE Perspective and Common Mistakes
Spring-mass systems and Hooke’s Law are crucial for JEE-level problems, often appearing in combined block-spring or oscillation questions.
A common pitfall is not considering the sign convention; always remember the force opposes displacement, so $F = -k x$.
For a comprehensive study of calculations and derivations, refer to Hooke's Law and Spring Force and practice integrating these concepts.
- Simple Harmonic Motion
- Elastic Potential Energy
- Series and Parallel Springs
- Oscillatory Systems
- Energy Conservation in Springs
- Damped and Forced Oscillations
FAQs on Understanding Spring Force and Hooke’s Law Made Simple
1. What is Hooke's Law?
Hooke's Law states that the force needed to extend or compress a spring by a certain distance is proportional to that distance.
- The relationship is given as F = -kx, where F is the spring force, k is the spring constant, and x is the extension or compression from the rest position.
- This law is valid within the elastic limit of the spring.
2. What is a spring force?
Spring force is the force exerted by a compressed or stretched spring upon any object attached to it.
- It always acts in a direction opposite to the displacement of the object from its equilibrium position.
- The magnitude of spring force depends on the spring constant and the amount of stretch or compression.
3. State the mathematical formula for Hooke's Law.
The mathematical formula for Hooke's Law is F = -kx.
- F: Restoring force exerted by the spring (in Newtons).
- k: Spring constant (measure of spring stiffness, in N/m).
- x: Displacement from equilibrium (in meters).
- The negative sign indicates the force acts in the opposite direction of displacement.
4. What is meant by spring constant?
Spring constant (k) is a measure of the stiffness or rigidity of a spring.
- A higher value of k means the spring is stiffer and requires more force to stretch or compress.
- Its SI unit is Newton per meter (N/m).
- It appears in the formula F = -kx.
5. Give an example to explain Hooke's Law in daily life.
A common example of Hooke's Law is the spring in a measuring scale like a weighing balance.
- When you place a weight on the pan, the spring stretches proportionally to the applied force (weight).
- The scale reading depends on the extension as per Hooke's Law: F = -kx.
6. Explain the terms 'elastic limit' and its significance in Hooke's Law.
Elastic limit is the maximum extent to which a material like a spring can be stretched or compressed and still return to its original shape once the force is removed.
- If the force exceeds the elastic limit, permanent deformation occurs and Hooke's Law is no longer valid.
- This ensures the law applies only for small deformations.
7. What happens if the force applied on a spring exceeds its elastic limit?
If the applied force goes beyond the spring's elastic limit, the spring undergoes permanent deformation.
- The spring will not return to its original length after removing the force.
- Hooke's Law does not apply in this case as the material behaves plastically.
8. List the factors affecting the spring constant (k).
The value of spring constant (k) depends on the following factors:
- Material of the spring
- Diameter of the wire used
- Diameter of the coil
- Number of turns or coils
- Length of the spring
9. Name two devices that work based on Hooke's Law.
Two common devices that operate using Hooke's Law are:
- Spring balances used for measuring force or weight
- Shock absorbers in automobiles
10. How can Hooke's Law be verified experimentally?
Hooke's Law can be verified by hanging different known weights on a spring and measuring its extension.
- Record the force applied (weight) and the extension each time.
- Plot a graph of force (F) vs. extension (x); a straight line confirms proportionality, validating Hooke's Law.
11. What is the unit of spring constant?
The SI unit of spring constant (k) is Newton per meter (N/m).
12. Why is the negative sign used in Hooke's Law?
The negative sign in F = -kx signifies that the restoring force of the spring always acts in the direction opposite to the displacement.
- This helps the spring return to its equilibrium position.
