Question

Plot a graph showing the variation of undecayed nuclei $N$ versus time $t$. From the graph, find out how one can determine the half-life and average life of the radioactive nuclei.

Answer 1

Hint: Radioactive decay is the process of slow disintegration of radioactive elements by releasing their energy in the form of radiation. The radioactive materials have unstable nuclei and therefore the nuclei breakdowns take place in the form of radiation. The radioactivity is given by the formula:
$A = - \dfrac{{dN}}{{dt}}$
where $A = $ total activity
$N = $ number of particles
 $t = $ time

Complete step by step solution:
In radioactive decay, the rate of radioactive decay is proportional to the number of nuclei present. The number of nuclei in radioactive decay degrades and exponentially decreases with time. As per the radioactive decay law, the disintegration equation is given by:
$N = {N_0}{e^{ - \lambda t}}$
Where, $N = $ number of radioactive atoms at any random time.
${N_0} = $ number of radioactive atoms present initially.
$\lambda = $ decay constant
$t = $ time

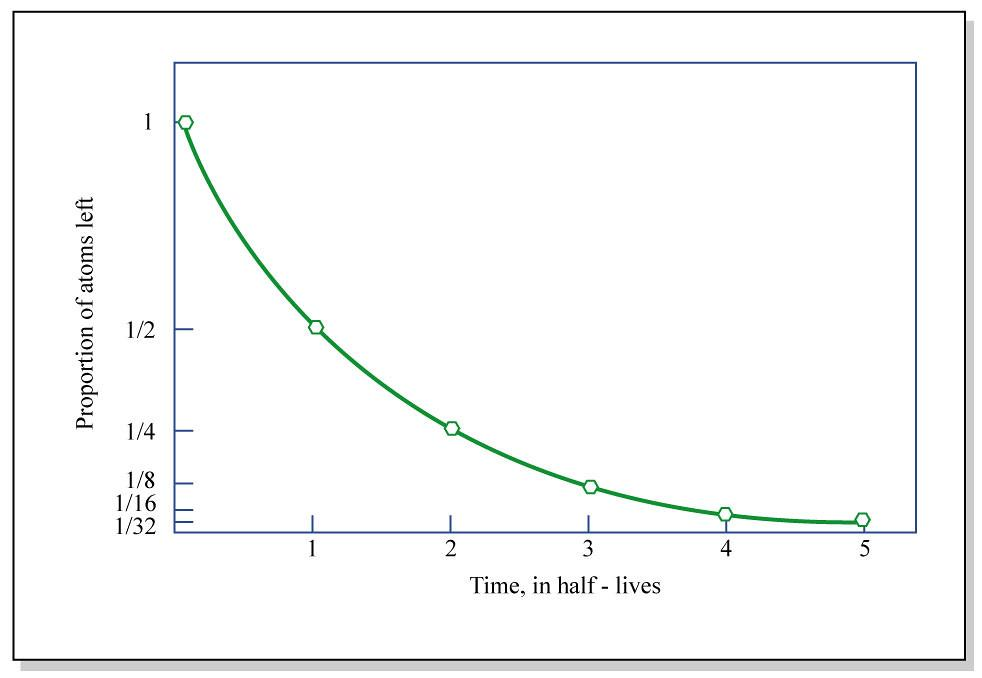
The above plot depicts the variation of the number of nuclei disintegrate with time. $N$ gradually decreases with increase in time and there comes a state where the nuclei are completely depleted at a given time. The rate of disintegration of nuclei is directly proportional to the nuclei available i.e. $ - \dfrac{{dN}}{{dt}} \propto N$
$ \Rightarrow - \dfrac{{dN}}{{dt}} = \lambda N$
The negative sign represents the gradual decrease of the number of nuclei with time.

The half-life of the radioactive element is the time required for its activity to decrease by one-half. So after one half-life, 50% of the initial activity remains and after two half-lives only 25% of the initial activity remains and after three half-lives, only 12.5% is present and so forth.
The half-life of a given nuclei can be derived as follows:
In half-life of a nuclei, the given lifespan of the nuclei is completed by 50% and it is denoted as ${t_{1/2}}$.
Therefore, the half-life of an atomic nuclei can be given by substituting $t = {t_{1/2}}$and $N = \dfrac{{{N_0}}}{2}$ in $N = {N_0}{e^{ - \lambda {t_{1/2}}}}$
Which gives, $\dfrac{{{N_0}}}{2} = {N_0}{e^{ - \lambda {t_{1/2}}}}$ $ \Rightarrow \dfrac{1}{2} = {e^{ - \lambda {t_{1/2}}}}$
Taking log on both side, we get ${\log _e}(2) = \lambda {t_{1/2}}$
$ \Rightarrow 0.693 = \lambda {t_{1/2}}$ $ \Rightarrow {t_{1/2}} = \dfrac{{0.693}}{\lambda }$
The average life of a nuclei atom is the amount of time required for the nuclei to decay to $36.8\% $ of the total amount. Therefore $N = 0.368{N_0}$ and $t$ changes as
$0.368{N_0} = {N_0}{e^{ - \lambda {t_{avg}}}}$
$ \Rightarrow 0.368 = {e^{ - \lambda {t_{avg}}}}$
Taking log on both sides,
${\log _e}(0.368) = - \lambda {t_{avg}}$
Which gives, $0.434 = \lambda {t_{avg}}$
$ \Rightarrow {t_{avg}} = \dfrac{{0.434}}{\lambda }$

Note: The unstable nuclei in radioactive samples do not decay simultaneously. Instead the decay of a given nucleus is an entirely random event. The rate of nuclei disintegration is insulated by surrounding electrons and hence the disintegration of the radioactive element is independent of temperature, pressure and doesn't follow any mass law or any other law that explains the physical and chemical change.