
PNP’ is the double ordinate of the parabola. Prove that the locus of the point of intersection of the normal at \[P\] and the diameter through \[{{P}^{'}}\] is equal to the parabola \[{{y}^{2}}=4a\left( x-4a \right)\].
Answer
126.9k+ views
Hint: The equation of diameter is given as \[y=\dfrac{2a}{m}\] , where \[m\] is the slope of the diameter.
A double ordinate is a chord which is perpendicular to the axis of the parabola .
Let the equation of the parabola be \[{{y}^{2}}=4ax\].
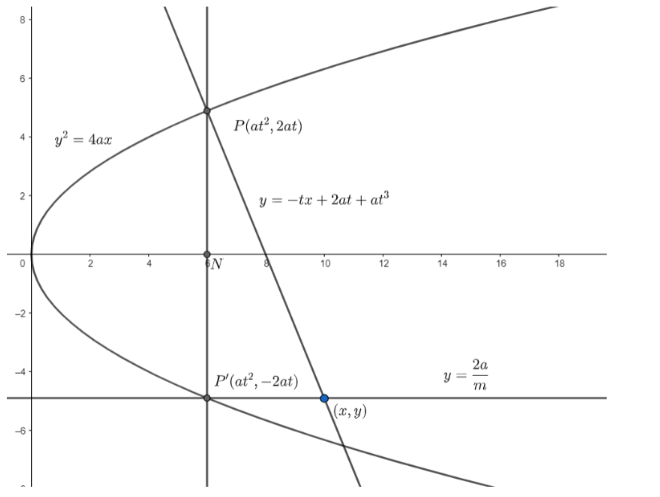
First , we need to find the equation of normal at \[P\].
We know the parametric coordinates of any point on the parabola can be written as \[P\left( a{{t}^{2}},2at \right)\].
Now , we know that a double ordinate is a chord which is perpendicular to the axis of the parabola .
So , the double ordinate of the point \[P\left( a{{t}^{2}},2at \right)\] will be \[{{P}^{'}}\left( a{{t}^{2}},-2at \right)\].
Now , we will find the equation of normal at \[P\].
We know, the equation of normal at \[\left( a{{t}^{2}},2at \right)\] is given as \[y=-tx+2at+a{{t}^{3}}\]
So , the equation of normal at \[P\] is given as \[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Now, we will find the equation of diameter at \[{{P}^{'}}\].
We know, the general equation of diameter is given as \[y=\dfrac{2a}{m}.....(ii)\], where \[m\] is the slope of the diameter.
Now , we will find the point of intersection of the normal and the diameter . Let this point be \[(x,y)\] .
In the question , it is given that the diameter passes through \[{{P}^{'}}\].
So , we will substitute \[y=-2at\] in equation \[(ii)\].
On substituting \[y=-2at\] in \[y=\dfrac{2a}{m}\], we get
\[-2at=\dfrac{2a}{m}\]
\[\Rightarrow m=\dfrac{-1}{t}\]
Now, we will substitute \[m=\dfrac{-1}{t}\] in \[(ii)\]. So, we get,
On substituting \[m=\dfrac{-1}{t}\] in \[(ii)\], we get,
\[y=-2at.....\left( iii \right)\]
Substituting \[y=-2at\] in \[\left( i \right)\], we get
\[-2at=-tx+2at+a{{t}^{3}}\]
Or, \[tx=4at+a{{t}^{3}}\]
Or, \[x=4a+a{{t}^{2}}....\left( iv \right)\]
Now , from \[\left( iii \right)\], we have
\[t=\dfrac{-y}{2a}\]
Now , we will substitute \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\].
On substituting \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\], we get
\[x=4a+a{{\left( \dfrac{-y}{2a} \right)}^{2}}\]
\[\Rightarrow x-4a=\dfrac{{{y}^{2}}}{4a}\]
\[\Rightarrow {{y}^{2}}=4a\left( x-4a \right)\]
Hence , the locus of the point of intersection of the normal at \[P\] and the diameter through \[{{P}^{'}}\] is equal to the parabola \[{{y}^{2}}=4a\left( x-4a \right)\].
Note: While substituting the values of \[m\] and \[t\], make sure the signs are correct. Students generally get confused in signs and make a mistake.
A double ordinate is a chord which is perpendicular to the axis of the parabola .
Let the equation of the parabola be \[{{y}^{2}}=4ax\].

First , we need to find the equation of normal at \[P\].
We know the parametric coordinates of any point on the parabola can be written as \[P\left( a{{t}^{2}},2at \right)\].
Now , we know that a double ordinate is a chord which is perpendicular to the axis of the parabola .
So , the double ordinate of the point \[P\left( a{{t}^{2}},2at \right)\] will be \[{{P}^{'}}\left( a{{t}^{2}},-2at \right)\].
Now , we will find the equation of normal at \[P\].
We know, the equation of normal at \[\left( a{{t}^{2}},2at \right)\] is given as \[y=-tx+2at+a{{t}^{3}}\]
So , the equation of normal at \[P\] is given as \[y=-tx+2at+a{{t}^{3}}....\left( i \right)\]
Now, we will find the equation of diameter at \[{{P}^{'}}\].
We know, the general equation of diameter is given as \[y=\dfrac{2a}{m}.....(ii)\], where \[m\] is the slope of the diameter.
Now , we will find the point of intersection of the normal and the diameter . Let this point be \[(x,y)\] .
In the question , it is given that the diameter passes through \[{{P}^{'}}\].
So , we will substitute \[y=-2at\] in equation \[(ii)\].
On substituting \[y=-2at\] in \[y=\dfrac{2a}{m}\], we get
\[-2at=\dfrac{2a}{m}\]
\[\Rightarrow m=\dfrac{-1}{t}\]
Now, we will substitute \[m=\dfrac{-1}{t}\] in \[(ii)\]. So, we get,
On substituting \[m=\dfrac{-1}{t}\] in \[(ii)\], we get,
\[y=-2at.....\left( iii \right)\]
Substituting \[y=-2at\] in \[\left( i \right)\], we get
\[-2at=-tx+2at+a{{t}^{3}}\]
Or, \[tx=4at+a{{t}^{3}}\]
Or, \[x=4a+a{{t}^{2}}....\left( iv \right)\]
Now , from \[\left( iii \right)\], we have
\[t=\dfrac{-y}{2a}\]
Now , we will substitute \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\].
On substituting \[t=\dfrac{-y}{2a}\] in equation \[\left( iv \right)\], we get
\[x=4a+a{{\left( \dfrac{-y}{2a} \right)}^{2}}\]
\[\Rightarrow x-4a=\dfrac{{{y}^{2}}}{4a}\]
\[\Rightarrow {{y}^{2}}=4a\left( x-4a \right)\]
Hence , the locus of the point of intersection of the normal at \[P\] and the diameter through \[{{P}^{'}}\] is equal to the parabola \[{{y}^{2}}=4a\left( x-4a \right)\].
Note: While substituting the values of \[m\] and \[t\], make sure the signs are correct. Students generally get confused in signs and make a mistake.
Recently Updated Pages
JEE Main 2025 - Session 2 Registration Open | Exam Dates, Answer Key, PDF

JEE Main 2023 (January 30th Shift 2) Maths Question Paper with Answer Key

JEE Main 2022 (July 25th Shift 2) Physics Question Paper with Answer Key

JEE Main 2023 (April 6th Shift 2) Maths Question Paper with Answer Key

Classification of Elements and Periodicity in Properties Chapter For JEE Main Chemistry

JEE Main 2023 (January 25th Shift 1) Maths Question Paper with Answer Key

Trending doubts
JEE Main Login 2045: Step-by-Step Instructions and Details

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

NCERT Solutions for Class 11 Maths Chapter 6 Permutations And Combinations Ex 6.4

JEE Main Course 2025: Get All the Relevant Details

Elastic Collisions in One Dimension - JEE Important Topic

JEE Main Chemistry Question Paper with Answer Keys and Solutions

NCERT Solutions Class 11 Maths Chapter 10 Conic Sections Exercise 10.4




