Question

Quarter part of a transparent cylinder ABC of radius \[R\] is kept on a horizontal floor and a horizontal beam of light falls on the cylinder in the two different arrangements of the cylinder as shown in the figure (a) and (b). in arrangement (a) light converges at point D, which is at a distance \[2R/m\] from B and in arrangement (b) light converges at point E, which is at a distance \[2R/\left( {m - 1} \right)\] from C. find out the refractive index of the material.
(A)

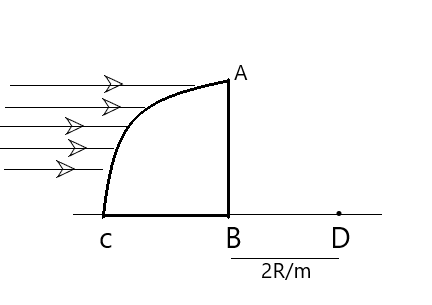
(B)

Answer 1

Hint: Since the light rays are parallel to each other, then object distance can be regarded as infinity. The point of focus of the ray is the image distance.
Formula used: In this solution we will be using the following formulae;
\[\dfrac{n}{v} - \dfrac{1}{u} = \dfrac{{n - 1}}{R}\]where \[n\] is the refractive index of the glass, \[v\] is the image distance, and \[u\] is the object distance in the first case, \[R\] is the radius of the glass, this is a thick lens equation for light striking the curve surface the Plano-convex.
\[\dfrac{1}{v} - \dfrac{n}{u} = \dfrac{{1 - n}}{R}\] this is the thick lens equation for when incident light strikes the flat surface of a Plano-convex lens.

Complete Step-by-Step solution:
For the first case, the light is incident on the curve side, hence, the governing equation can be given be given by
\[\dfrac{n}{{{v_1}}} - \dfrac{1}{{{u_1}}} = \dfrac{{n - 1}}{R}\] where \[n\] is the refractive index of the glass, \[{v_1}\] is the image distance in the first case, and \[{u_1}\] is the object distance in the first case, \[R\] is the radius of the glass.
Since the light rays were parallel to each other, then the object distance can be regarded as infinity, hence
\[\dfrac{n}{{{v_1}}} - \dfrac{1}{\infty } = \dfrac{{n - 1}}{R}\]
\[ \Rightarrow \dfrac{n}{{{v_1}}} = \dfrac{{n - 1}}{R}\]
The point of convergence is the image distance, hence as given in question
\[\dfrac{n}{{\dfrac{{2R}}{m}}} = \dfrac{{n - 1}}{R}\]
Hence, by simplifying and cancelling \[R\] we have
\[mn = 2\left( {n - 1} \right)\]
For the second case, the light is incident on the flat part of the glass, hence, the governing equation is given by
\[\dfrac{1}{{{v_2}}} - \dfrac{n}{{{u_2}}} = \dfrac{{1 - n}}{R}\]
Hence, since light is parallel again, and the point of convergence is \[\dfrac{R}{{m - 1}}\], hence, by substitution, we have
\[\dfrac{1}{{\dfrac{R}{{m - 1}}}} - \dfrac{n}{\infty } = \dfrac{{1 - n}}{R}\]
By simplifying, we get
\[\dfrac{{m - 1}}{R} = \dfrac{{1 - n}}{{ - R}}\]
\[ \Rightarrow m - 1 = 1 - n\]
Then, we see that
\[m = 2 - n\]
Inserting this expression into the equation \[mn = 2\left( {n - 1} \right)\], we get
\[\left( {2 - n} \right)n = 2\left( {n - 1} \right)\]
\[ \Rightarrow 2n - {n^2} = 2n - 2\]
By cancelling and simplifying, we get
\[{n^2} = 2\]
\[ \Rightarrow n = 1.4\]

Note: For clarity, observe that the equation \[\dfrac{n}{v} - \dfrac{1}{u} = \dfrac{{n - 1}}{R}\], for example, is very similar to the lens maker equation \[\dfrac{1}{f} = n - 1\left( {\dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}} \right)\]. But since the surface is flat, we have that one of the radius be equal to infinity reducing the equation to \[\dfrac{1}{f} = n - 1\left( {\dfrac{1}{{{R_1}}}} \right)\] then \[\dfrac{1}{f}\] can be proven to be \[\dfrac{n}{v} - \dfrac{1}{u}\]. Similar case for the second equation.