Question

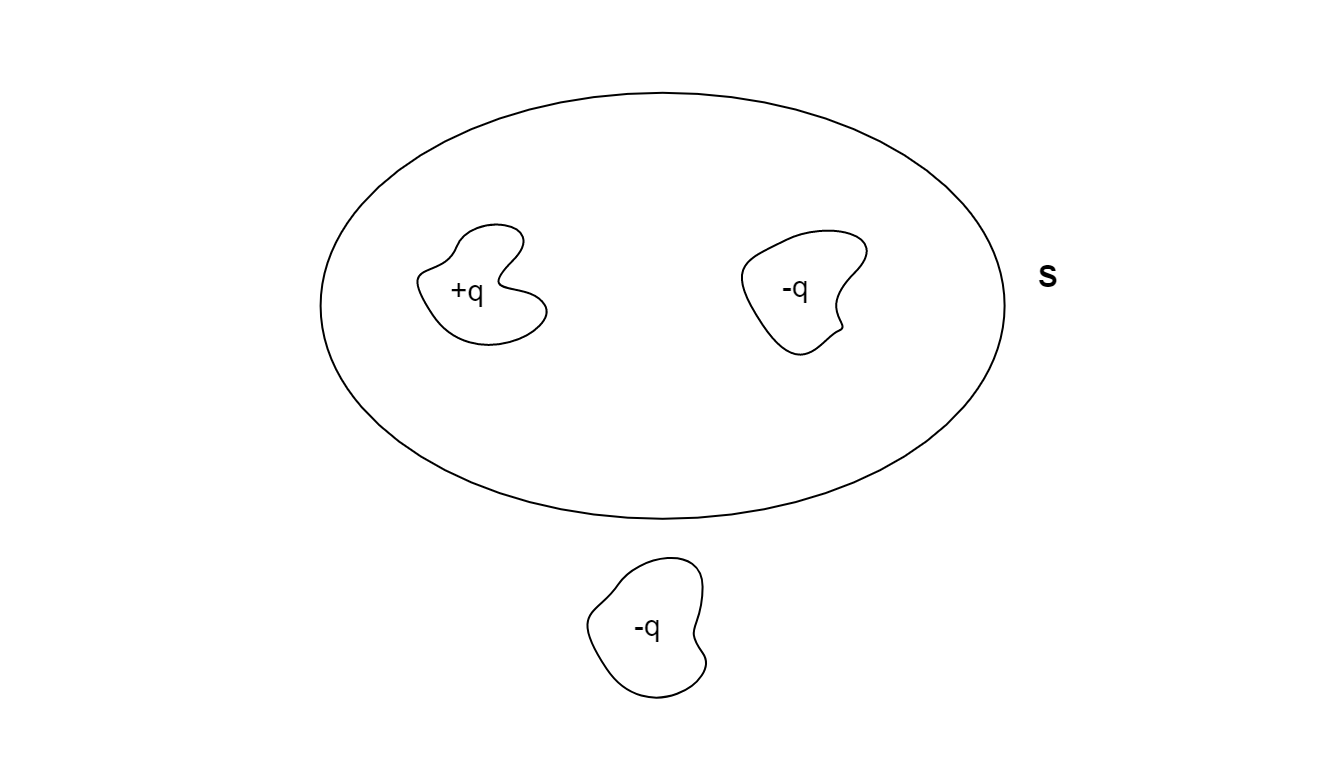
Shown below is a distribution of charges. What is the flux of the electric field due to these charges through the surface $S$?

Answer 1

Hint: We will first learn about the electric flux. Then we will think about how it can change with other variations. We have to think about whether it depends on the given charge that is not bounded by the surface or not. If we get our concepts clear on this, then we are good to figure out the answers.

Formula used:
$\phi = \dfrac{{{q_{net}}}}{{{ \varepsilon _0}}}$

Complete step by step solution:
In electrostatics, we have learned about the electric field lines. These imaginary lines can show us the electric field's direction produced by the electric charge.
In general, we can define the electric flux as the number of electric field lines through a unit area bounding the electric charge. Like the surface vector, it is a vector quantity that directs normal towards the surface.
We have electric flux through a closed surface $S$,
$\phi = \dfrac{{{q_{net}}}}{{{ \varepsilon _0}}}$ ……….$(1)$
${q_{net}}$ is the total electric charge surrounded by the surface
${ \varepsilon _0}$ is the electrical permittivity of vacuum
It is now clear that the charge outside the surface will not affect the electric flux.
So the total charge surrounded by the surface $S$ is-
$\Rightarrow {q_{net}} = \left( { + q} \right) + \left( { - q} \right)$
$ \Rightarrow {q_{net}} = 0$
Hene we put this in the equation $(1)$ and get-
$\Rightarrow \phi = \dfrac{0}{{{ \varepsilon _0}}}$
$ \Rightarrow \phi = 0$

Therefore, the electric flux through the closed surface is equal to $0$.

Note: The electric flux is a way of describing the electric field strength at any point from the electric charge, causing the electric field. At any elementary point on the surface, electric flux is the dot product of the electric field and the elementary surface vector. The S.I. unit of electric flux is $N.{m^2}.{C^{ - 1}}$ , and its dimensional formula is $\left[ {M{L^3}{T^{ - 3}}{I^{ - 1}}} \right]$.