Question

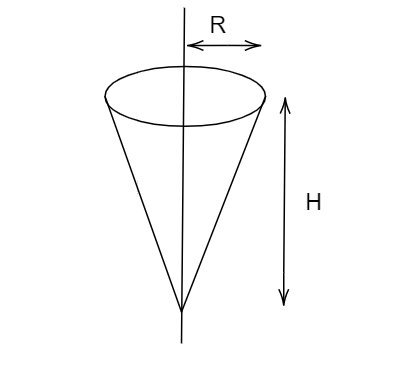
Shown in the figure is a hollow ice cream cone (it is open at the top). If its mass is M, the radius of its top, R and height, H, then find the moment of inertia about its axis.

A. \[\dfrac{{M{R^2}}}{2}\]
B. \[\dfrac{{M{R^2}}}{3}\]
C. \[\left[ {\dfrac{{M\left( {{R^2} + {H^2}} \right)}}{4}} \right]\]
D. \[\dfrac{{M{H^2}}}{3}\]

Answer 1

Hint:Before we proceed into this problem it is important to know about the moment of inertia. It is defined as the quantitative measure of the rotational inertia of a body.

Formula Used:
Moment of inertia about an axis ON is given by,
\[{I_{ON}} = \int {dm \times {r^2}} \]
Where, \[dm\] is mass of the differential element, \[r\] is radius of the differential element.

Complete step by step solution:
The slant height of this cone is ‘l’ with the radius of the cone R and the height of the cone is H as shown in the diagram.

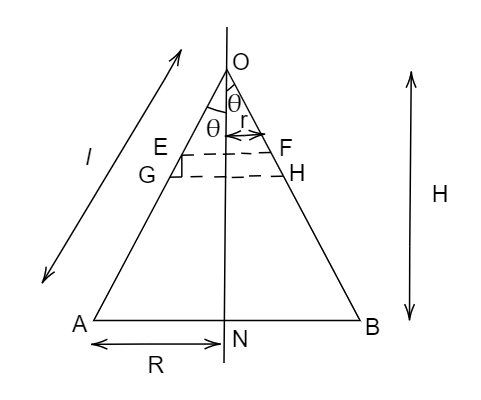
Image: A hollow ice cream cone


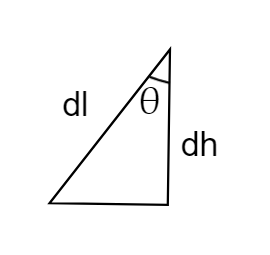
Image: Enlarged view

Now let’s take a differential element as shown in the dotted line. The slant of the height of the differential element is dl, radius r, and height from the apex is h. Let’s consider a triangle in the differential element as shown in the diagram.
Then, \[\cos \theta = \dfrac{{dh}}{{dl}}\]
\[dl = \dfrac{{dh}}{{\cos \theta }}\]

Now we have to find the moment of inertia. If we find the moment of inertia of this differential element, after that we can integrate it to get the moment of inertia of the whole cone.
We know that,
Area of the cone \[ = \pi Rl\]
\[ = \pi R\sqrt {{H^2} + {R^2}} \]

Now, apply Pythagoras theorem to the triangle OAN we get,
\[l = \sqrt {{H^2} + {R^2}} \]………(1)
Also, the area of the element= area of the rectangle EFGH
i.e., the Area of the element \[ = 2\pi rdl\]
By substituting the value \[dl\] we obtain,
Area of the element \[ = 2\pi r\dfrac{{dh}}{{\cos \theta }}\]
Suppose \[\dfrac{M}{A} = \lambda \]
Mass of the element, \[dm = \lambda \times \text{(area of element)}\]
\[dm = \lambda \times \left( {2\pi r\dfrac{{dh}}{{\cos \theta }}} \right)\]
Substituting the value of \[\lambda \] and area of the cone we get,
\[dm = \dfrac{M}{{\pi Rl}} \times \left( {2\pi r\dfrac{{dh}}{{\cos \theta }}} \right)\]

From triangle OMF, \[\tan \theta = \dfrac{r}{h}\]
\[ \Rightarrow r = h\tan \theta \]
\[dm = \dfrac{{2M\left( {h\tan \theta } \right)dh}}{{Rl\cos \theta }}\]
We have calculated the mass of different elements.
Now calculate the moment of inertia about an axis ON.
\[{I_{ON}} = \int {dm \times {r^2}} \]
\[{I_{ON}} = \int {\dfrac{{2M\left( {h\tan \theta } \right)dh{{\left( {h\tan \theta } \right)}^2}}}{{Rl\cos \theta }}} \]
Substitute the value of ‘l’ from the equation (1) we get,
\[{I_{ON}} = \int {\dfrac{{2M\left( {h\tan \theta } \right)dh{{\left( {h\tan \theta } \right)}^2}}}{{R\sqrt {{R^2} + {H^2}} \cos \theta }}} \]

Rearrange the above equation and integrate it from the limits 0 to R we get,
\[{I_{ON}} = \dfrac{{2M{{\tan }^3}\theta }}{{R\sqrt {{R^2} + {H^2}} \cos \theta }}\int\limits_0^H {{h^3}dh} \]
\[{I_{ON}} = \dfrac{{2M{{\tan }^3}\theta }}{{R\sqrt {{R^2} + {H^2}} \cos \theta }}\left[ {\dfrac{h}{4}} \right]_0^H\]
From the triangle OAN,
\[\tan \theta = \dfrac{R}{H}\], \[\cos \theta = \dfrac{H}{{\sqrt {{H^2} + {R^2}} }}\]
\[{I_{ON}} = \dfrac{{2M{{\left( {\dfrac{R}{H}} \right)}^3}}}{{R\sqrt {{R^2} + {H^2}} \left( {\dfrac{H}{{\sqrt {{R^2} + {H^2}} }}} \right)}}\dfrac{{{H^4}}}{4}\]
On simplifying the above equation we get,
\[\therefore {I_{ON}} = \dfrac{{M{R^2}}}{2}\]
Therefore, the moment of inertia about its axis ON is, \[\dfrac{{M{R^2}}}{2}\].

Hence, Option A is the correct answer

Note:In physics, a moment of inertia is a quantitative measure of a body's rotational inertia—that is, the resistance that the body shows to having its speed of rotation along an axis altered by the application of a torque. The moment of inertia depends on the mass, axis of rotation, shape and size of the body.