
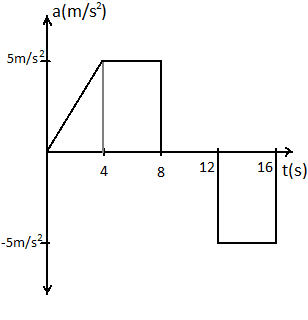
The acceleration of a train between two stations is shown in the figure. The maximum speed of the train is:
A)
B)
C)
D)
Answer
140.4k+ views
Hint: Define acceleration and try to recall the mathematical expression of acceleration. From the graph and from the relation between velocity and acceleration we can easily estimate the maximum speed the train can reach.
Complete step by step solution:
Let’s have some nostalgia and revisit our classes of kinematics. Our physics teacher was yelling that acceleration is the rate of change of velocity.
For a small change in velocity
Further simplifying,
For the maximum velocity, we can integrate both sides of the above equation.
Taking integration both sides, we get
This is the expression for velocity in terms of acceleration.
Now we know that integrating a function/ curve, we get the area under that function/ curve. Thus from equation (2), we can conclude that the area under the acceleration-time graph is defined as the velocity of the train/ moving object.
Now from the diagram given in the question, we can see that after
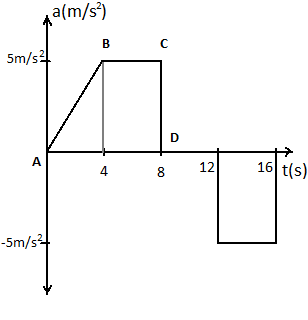
From the above diagram the area of the section
Area of
Area of
Area of rectangle
Thus the maximum velocity of the train would be
So the correct answer is option B.
Note: Using this technique we can solve problems where we are provided with a graph in simple kinematics, for example, in a velocity time graph, the area under the graph represents the displacement of the moving body. Because the rate of change of displacement is defined as velocity.
Complete step by step solution:
Let’s have some nostalgia and revisit our classes of kinematics. Our physics teacher was yelling that acceleration is the rate of change of velocity.
For a small change in velocity
Further simplifying,
For the maximum velocity, we can integrate both sides of the above equation.
Taking integration both sides, we get
This is the expression for velocity in terms of acceleration.
Now we know that integrating a function/ curve, we get the area under that function/ curve. Thus from equation (2), we can conclude that the area under the acceleration-time graph is defined as the velocity of the train/ moving object.
Now from the diagram given in the question, we can see that after

From the above diagram the area of the section
Area of
Area of
Area of rectangle
Thus the maximum velocity of the train would be
So the correct answer is option B.
Note: Using this technique we can solve problems where we are provided with a graph in simple kinematics, for example, in a velocity time graph, the area under the graph represents the displacement of the moving body. Because the rate of change of displacement is defined as velocity.
Recently Updated Pages
Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

Motion in a Straight Line Class 11 Notes: CBSE Physics Chapter 2

Important Questions for CBSE Class 11 Physics Chapter 1 - Units and Measurement

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




