Question

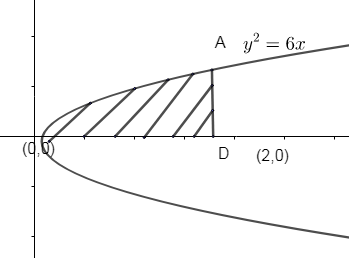
The area of the circle \[{{x}^{2}}+{{y}^{2}}=16\] exterior to the parabola \[{{y}^{2}}=6x\]is
a). \[\dfrac{4}{3}\left( 4\pi -\sqrt{3} \right)\]
b). \[\dfrac{4}{3}\left( 8\pi -\sqrt{3} \right)\]
c). \[\dfrac{4}{3}\left( 4\pi +\sqrt{3} \right)\]
d). \[\dfrac{4}{3}\left( 8\pi +\sqrt{3} \right)\]

Answer 1

Hint: Substitute \[{{y}^{2}}=6x\] in the equation of circle \[{{x}^{2}}+{{y}^{2}}=16\] and find the value of x and find the points which intersects parabola with circle. Thus, to find the required area, subtract the area of the circle with the area of the parabola which is exterior to the circle.

Complete step-by-step solution:
First, we will draw the corresponding figure,
draw the circle \[{{x}^{2}}+{{y}^{2}}=16\], where center is (0, 0).
Radius of the circle = \[r=\sqrt{16}=4\]
And draw the parabola, \[{{y}^{2}}=6x\].


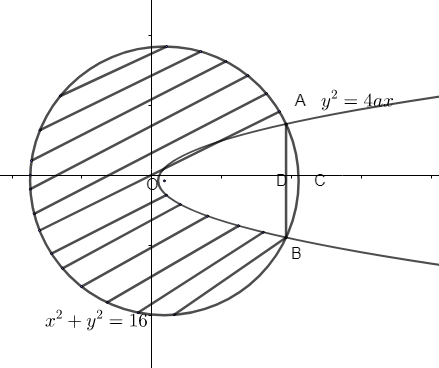
Now, we need to find the intersection A and B i.e., the intersection points of the parabola with the circle.
We know, \[{{y}^{2}}=6x\], put the value of \[{{y}^{2}}\]in the equation of circle, we get
\[\begin{align}
  & \Rightarrow {{x}^{2}}+{{y}^{2}}=16 \\
 & \Rightarrow {{x}^{2}}+6x=16 \\
 & \Rightarrow {{x}^{2}}+6x-16=0-(1) \\
\end{align}\]
Equation (1) represents a quadratic equation, similar to the general equation \[a{{x}^{2}}+bx+c=0\]. By comparing them we get,
\[\therefore a=1,b=6,c=-16\]
Substitute the values in \[\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\], we get
\[\begin{align}
  & =\dfrac{-6\pm \sqrt{{{6}^{2}}-4\times 1\times \left( -16 \right)}}{2}=\dfrac{-6\pm \sqrt{36+64}}{2}=\dfrac{-6\pm \sqrt{100}}{2} \\
 & =\dfrac{-6\pm 10}{2} \\
\end{align}\]
\[\therefore \]We get the roots as \[\left( \dfrac{-6+10}{2} \right)\] and \[\left( \dfrac{-6-10}{2} \right)\].
That is the roots are 2 and -8.
So, we have x = 2 and x = -8, substitute them in the equation of parabola, we get
\[\begin{align}
  & x=2\Rightarrow {{y}^{2}}=6x=6\times 2=12 \\
 & y=\pm \sqrt{12}=\pm 2\sqrt{3} \\
 & x=-8\Rightarrow {{y}^{2}}=6\times \left( -8 \right)=-32 \\
\end{align}\]
Since, the square cannot be negative, x = -8 is not possible.
\[\therefore \]Point A is \[\left( 2,2\sqrt{3} \right)\] and \[B\left( 2,-2\sqrt{3} \right)\].
Now we will find the required area, from figure we see that
Required area = Area of circle – Area OACB
Now, we need to find the area of the circle.



Area of circle\[=4\times \]Area of 1st quadrant
\[=4\times \int\limits_{0}^{4}{ydx}\]
We have to get the value of y from the equation of the circle
\[\begin{align}
  & {{x}^{2}}+{{y}^{2}}=16 \\
 & \Rightarrow {{y}^{2}}=16-{{x}^{2}} \\
 & \therefore y=\pm \sqrt{16-{{x}^{2}}} \\
\end{align}\]
Since, we need to find the area of the $1^{st}$ quadrant, we take y positive.
\[\therefore y=\sqrt{16-{{x}^{2}}}-(1)\]
\[\therefore \]Area of the circle\[=4\times \int\limits_{0}^{4}{\sqrt{16-{{x}^{2}}}dx}\]
\[=4\int\limits_{0}^{4}{\sqrt{{{4}^{2}}-{{x}^{2}}}dx}\]
We know the formula,
\[\int{\sqrt{{{a}^{2}}-{{x}^{2}}}}dx=\dfrac{x}{2}\sqrt{{{a}^{2}}-{{x}^{2}}}+\dfrac{{{a}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{a}+c-(2)\]
Replace a by 4, we get
\[\therefore \]Area of circle \[=4\left[ \dfrac{x}{2}\sqrt{{{4}^{2}}-{{x}^{2}}}+\dfrac{{{4}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{4} \right]_{0}^{4}\]
Area of circle \[=4\left[ \dfrac{x}{2}\sqrt{16-{{x}^{2}}}+8{{\sin }^{-1}}\dfrac{x}{4} \right]_{0}^{4}\]
Applying the limits, we get
\[\begin{align}
  & =4\left[ \left( \dfrac{4}{2}\sqrt{16-{{4}^{2}}}+8{{\sin }^{-1}}\dfrac{4}{4} \right)-\left( \dfrac{0}{2}\sqrt{{{16}^{2}}-{{0}^{2}}}+8{{\sin }^{-1}}\dfrac{0}{4} \right) \right] \\
 & =4\left[ 0+8{{\sin }^{-1}}1-0-8{{\sin }^{-1}}0 \right] \\
 & =4\times \left[ 0+8\times \dfrac{\pi }{2}-0-0 \right]=4\times 8\times \dfrac{\pi }{2}=16\pi -(3) \\
\end{align}\]
Now, we need to find the area of OACB. OACB is symmetric about the y-axis.
\[\therefore \]area OACB\[=2\times \]area OAC.

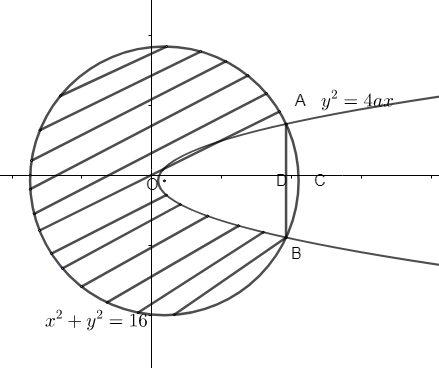
Area OAC = area OAD + area ADC [from figure]
So, we get
\[\therefore \]area OACB = 2(area OAD + area ADC)……..(A)
Now we will find all the areas separately.
Area ACD
As x-coordinate of point A is ‘2’ and x-coordinate of point C is ‘4’, so
Area ACD\[=\int\limits_{2}^{4}{ydx}\]

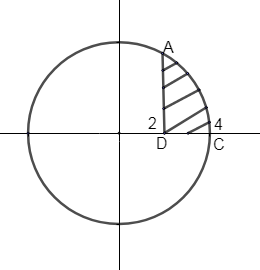
As we are taking $1^{st}$ quadrant
\[y=\sqrt{16-{{x}^{2}}}\]
\[\therefore\] area ACD\[=\int\limits_{2}^{4}{\sqrt{16-{{x}^{2}}}dx}=\int\limits_{2}^{4}{\sqrt{{{4}^{2}}-{{x}^{2}}}dx}\]
Use the formula mentioned in equation (2), we get
Area ACD\[=\left[ \dfrac{x}{2}\sqrt{{{4}^{2}}-{{x}^{2}}}+\dfrac{{{4}^{2}}}{2}{{\sin }^{-1}}\dfrac{x}{4} \right]_{2}^{4}\]
Applying the limits, we get
\[\begin{align}
  & =\left[ \left( \dfrac{4}{2}\sqrt{{{4}^{2}}-{{4}^{2}}}+8{{\sin }^{-1}}\dfrac{4}{4} \right)-\left( \dfrac{2}{2}\sqrt{{{4}^{2}}-{{2}^{2}}}+\dfrac{{{4}^{2}}}{2}{{\sin }^{-1}}\dfrac{2}{4} \right) \right] \\
 & =0+8{{\sin }^{-1}}1-2\sqrt{3}-8\times {{\sin }^{-1}}\dfrac{1}{2} \\
 & =8\times \dfrac{\pi }{2}-2\sqrt{3}-8\times \dfrac{\pi }{6} \\
 & =4\pi -\dfrac{4\pi }{3}-2\sqrt{3} \\
 & =\dfrac{12\pi -4\pi }{3}-2\sqrt{3} \\
\end{align}\]
Area ACD\[=\dfrac{8\pi }{3}-2\sqrt{3}\]-(4)
Now we will find the Area CAD\[=\int\limits_{0}^{2}{ydx}\]

We have to find y from the equation of parabola.
\[\begin{align}
  & {{y}^{2}}=6x\Rightarrow y=\pm \sqrt{6x} \\
 & \therefore y=\sqrt{6x} \\
\end{align}\]
Therefore, the area OAD will become,
\[=\int\limits_{0}^{2}{\sqrt{6x}dx}\]
Taking out the constant, we get
\[=\sqrt{6}\int\limits_{0}^{2}{\sqrt{x}.dx}=\sqrt{6}\int\limits_{0}^{2}{{{x}^{\dfrac{1}{2}}}dx}\]
On integrating, we get
\[\begin{align}
  & =\sqrt{6}\left[ \dfrac{{{x}^{\dfrac{1}{2}+1}}}{\dfrac{1}{2}+1} \right]_{0}^{2} \\
 & =\sqrt{6}{{\left[ \dfrac{{{x}^{\dfrac{3}{2}}}}{\dfrac{3}{2}} \right]}^{2}} \\
 & =\dfrac{2\sqrt{6}}{3}\left[ {{x}^{\dfrac{3}{2}}} \right]_{0}^{2} \\
\end{align}\]
On Applying the limits and solving, we get
\[\begin{align}
  & =\dfrac{2\sqrt{6}}{3}\times \left[ {{2}^{\dfrac{3}{2}}}-{{0}^{\dfrac{3}{2}}} \right] \\
 & =\dfrac{2\sqrt{6}}{3}\times {{2}^{\dfrac{3}{2}}} \\
 & =\dfrac{2\sqrt{2}\times \sqrt{3}}{3}\times 2\sqrt{2} \\
 & =\dfrac{4\times 2}{\sqrt{3}} \\
\end{align}\]
Therefore, the area of OAD wil be\[=\dfrac{8}{\sqrt{3}}-(5)\]
Now consider equation (A), we get
\[\therefore \]area OACB = 2(area OAD + area ADC)……..(A)
Substituting values from equation (4) and (5), we get
\[\therefore \]Area OACB \[=2\left( \dfrac{8}{\sqrt{3}}+\dfrac{8\pi }{3}-2\sqrt{3} \right)\]
On solving this we get
\[\therefore \]Area OACB \[=2\left( \dfrac{8}{\sqrt{3}}\times \dfrac{\sqrt{3}}{\sqrt{3}}+\dfrac{8\pi }{3}-2\sqrt{3} \right)=2\left( \dfrac{8\sqrt{3}}{3}+\dfrac{8\pi }{3}-2\sqrt{3} \right)\]
Taking the LCM, we get
\[\therefore \]Area OACB \[=2\left( \dfrac{8\sqrt{3}+8\pi -2\sqrt{3}\times 3}{3} \right)\]
\[\therefore \]Area OACB \[=2\left( \dfrac{2\sqrt{3}+8\pi }{3} \right)\]
\[\therefore \]Required area = Area of circle – area OACB
Required area \[=16\pi -2\left( \dfrac{2\sqrt{3}+8\pi }{3} \right)\]
Required area \[=\left( \dfrac{16\pi \times 3-4\sqrt{3}-16\pi }{3} \right)\]
Required area \[=\left( \dfrac{32\pi -4\sqrt{3}}{3} \right)\]
\[\therefore \] Required area is \[\dfrac{4}{3}\left( 8\pi -\sqrt{3} \right)\] square units.
Hence, the correct option is (c).

Note: We know the formula for finding the area of circle \[=\pi {{r}^{2}}\] , we can find the radius from the equation given to us, i.e., \[{{x}^{2}}+{{y}^{2}}=16\]. Hence, from this, we get the radius as 4. Now apply this radius directly in the formula for finding the area of a circle as,
Area of circle \[=\pi \times {{4}^{2}}=16\pi \]. Hence, you can also find the area using this simple formula.