Question

The bob of a simple pendulum performs S.H.M. with period ‘T’ in air and with period ‘\[{T_1}\]’ in water. Relation between ‘T’ and ‘\[{T_1}\]’ is (neglect the friction due to water, density of the material of the bob is $\dfrac{9}{8} \times {10^3}kg/{m^3}$ , density of water =$1g/cc$)
(A) ${T_1} = 3T$
(B) ${T_1} = 2T$
(C) ${T_1} = T$
(D) ${T_1} = \dfrac{T}{2}$

Answer 1

Hint Consider two cases of time periods. Calculate the effective g and find its relation with g in air. Since given data is in terms of density the mass is converted in terms of density as well. Then substitute the given data to obtain a relation between the two time periods.

Complete step-by-step solution


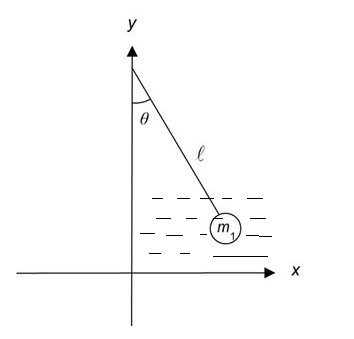
T and \[{T_1}\]are the time period of the simple pendulum in air and water respectively.

We know that the time period of the pendulum is,
$T = 2\pi \sqrt {\dfrac{l}{g}} $
The length of the pendulum l remains the same in both mediums but g is not the same so we need to consider an effective value
\[{g_e}\] for\[{T_1}\]
\[{g_e}\] is given by the difference between the weight of the bob and the buoyancy force when in water.
${g_e} = \dfrac{{mg - {f_b}}}{m}$
Here,
m is the mass of the bob
g is the acceleration due to gravity
\[{F_b}\] is the buoyancy force= mass of water displaced \[ \times {\text{ }}g\]

Mass is written in terms of density \[\rho \] using the formula,
$\rho = \dfrac{m}{V}$
${g_e} = \dfrac{{\rho Vg - {\rho _1}Vg}}{{\rho V}} = \dfrac{{g\left( {\rho - {\rho _1}} \right)}}{\rho }$
Where,
 \[\rho \]is the density of the material of the bob $\dfrac{9}{8} \times {10^3}kg/{m^3}$

\[{\rho _1}\] is the density of water $1g/cc$
On substituting the values,
$
  {g_e} = \dfrac{{\left( {\dfrac{9}{8} \times {{10}^3} - 1 \times {{10}^3}} \right)g}}{{\dfrac{9}{8} \times {{10}^3}}} \\
  {g_e} = \dfrac{g}{9} \\
 $

Since,
 ${T_1} = 2\pi \sqrt {\dfrac{l}{{{g_e}}}} $
Now, substitute the value of \[{g_e}\] in the above equation, we get,
$
  {T_1} = 2\pi \sqrt {\dfrac{{l9}}{g}} = 3\left( {2\pi \sqrt {\dfrac{l}{g}} } \right) \\
  \therefore {T_1} = 3T \\
 $

Hence, the correct option is A.

Note The pendulum in water displaces some volume so it has to be considered to calculate the time period. Time period is the time taken to complete one oscillation about the mean position. It depends on the medium in which it is oscillating.