Question

The box of a pinhole camera of length $L$ , has a hole of a radius $a$ . It is assumed when the hole is illuminated by a parallel beam of light of wavelength $\lambda $ the spread of the spot (obtained on the opposite wall of the camera) is the sum of its geometrical spread and the spread due to diffraction. The spot would then have its minimum size say ${b_{\min }}$ when:
(A) $a = \dfrac{{{\lambda ^2}}}{L}$ and ${b_{\min }} = \dfrac{{2{\lambda ^2}}}{L}$
(B) $a = \sqrt {\lambda L} $and ${b_{\min }} = \dfrac{{2{\lambda ^2}}}{L}$
(C) $a = \sqrt {\lambda L} $ and ${b_{\min }} = \sqrt {4\lambda L} $
(D) $a = \dfrac{{{\lambda ^2}}}{L}$ and ${b_{\min }} = \sqrt {4\lambda L} $

Answer 1

Hint: In this problem, it is given that a hole of the pinhole camera box is illuminated by a parallel beam of light and that light got spread due to diffraction and observed on the opposite wall of the camera box making a geometrical pattern. By understanding this geometrical representation and diffraction pattern we will try to solve this problem.

Complete step by step answer:
Here given that the spread of the spot is the sum of geometric spread and spread due to diffraction

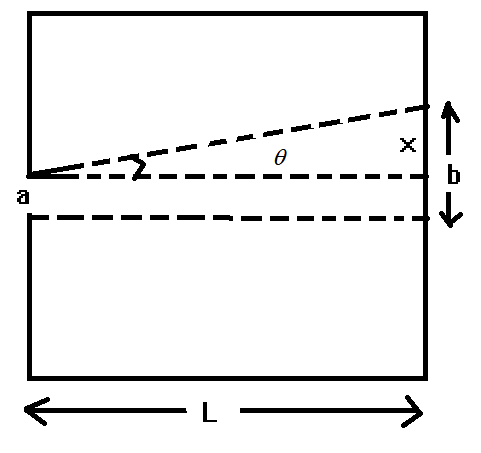
From the figure, we can see that geometrical spread = diffraction width $a$ + spread due to diffraction
Here $\sin \theta = x/L$
$ \Rightarrow x = L\sin \theta $
As the angle is very small
$x \approx L\theta $
Now $\theta = \dfrac{\lambda }{a}$ for the angle of diffraction
where $\lambda $is wavelength and $a$ is the width
$x = L\dfrac{\lambda }{a}$
Geometrical spread $(b)$ = diffraction width $a$ + spread due to diffraction $(x)$
$ \Rightarrow b = a + x$
$ \Rightarrow b = a + L\dfrac{\lambda }{a}$ ------------------- Equation $(1)$
As we know that the minimum deviation $({b_{\min }})$ is given as $\dfrac{{db}}{{da}} = 0$
Now differentiating the equation $(1)$ with respect to $a$
$\dfrac{{db}}{{da}} = \dfrac{d}{{da}}\left( {a + L\dfrac{\lambda }{a}} \right)$
$ \Rightarrow \dfrac{{db}}{{da}} = 1 - \dfrac{{\lambda L}}{{{a^2}}}$
As the minimum deviation is given by $\dfrac{{db}}{{da}} = 0$
$1 - \dfrac{{\lambda L}}{{{a^2}}} = 0$
$ \Rightarrow \dfrac{{\lambda L}}{{{a^2}}} = 1$
Upon rearranging the equation we get,
${a^2} = \lambda L$
$\therefore a = \sqrt {\lambda L} $
Now substituting the value of $a$in equation $(1)$ we will get ${b_{\min }}$
${b_{\min }} = a + L\dfrac{\lambda }{a}$
$ \Rightarrow {b_{\min }} = \sqrt {\lambda L} + L\dfrac{\lambda }{{\sqrt {\lambda L} }}$
Which results in ${b_{\min }}$as
${b_{\min }} = 2\sqrt {\lambda L} $
$\therefore {b_{\min }} = \sqrt {4\lambda L} $
Therefore the spot would then have its minimum size say ${b_{\min }} = \sqrt {4\lambda L} $, when$a = \sqrt {\lambda L} $ .

Hence the option (C) is the correct answer.

Additional information: The diffraction is a phenomenon of deviation of bending of the light beam by the edge of any object when it passes by it. When the light encounters any obstacles it gets slightly bent by the corner of those obstacles. Diffraction can be seen regularly in day-to-day life for example rainbow patterns are observed on CDs and DVDs, the pencil placed in a glass filled with water looks bent.

Note: We know that the angle of diffraction depends on the size of the width of the slit. Here in the above calculation, we have taken $\sin \theta \approx \theta $because the angle of diffraction is very small as we are illuminating a pinhole that is acting as a slit for the incoming light.