
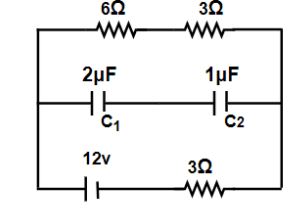
The charges stored in each capacitor
Answer
138.9k+ views
Hint: Find out the current flowing through the circuit which is given by the ratio of voltage to the equivalent resistance
Complete step-by-step answer:
Consider the capacitors as fully charged, then current is not drawn from the cell.
The equivalent resistance of the circuit is
Current of the circuit is given by,
Given that,
Hence the current in the circuit is 1A.
Now the potential across the capacitors is
The net capacitance between them is
Now the equivalent charge is given by
The capacitors are in series so the charge will be the same on both capacitors that is
The correct option is A.
Note: the effective capacitance in parallel grouping is given by,
For n identical capacitors in series,
In parallel,
Complete step-by-step answer:
Consider the capacitors as fully charged, then current is not drawn from the cell.
The equivalent resistance of the circuit is
Current of the circuit is given by,
Given that,
Hence the current in the circuit is 1A.
Now the potential across the capacitors is
The net capacitance between them is
Now the equivalent charge is given by
The capacitors are in series so the charge will be the same on both capacitors that is
The correct option is A.
Note: the effective capacitance in parallel grouping is given by,
For n identical capacitors in series,
In parallel,
Recently Updated Pages
Young's Double Slit Experiment Step by Step Derivation

How to find Oxidation Number - Important Concepts for JEE

How Electromagnetic Waves are Formed - Important Concepts for JEE

Electrical Resistance - Important Concepts and Tips for JEE

Average Atomic Mass - Important Concepts and Tips for JEE

Chemical Equation - Important Concepts and Tips for JEE

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Physics Average Value and RMS Value JEE Main 2025

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main

Displacement-Time Graph and Velocity-Time Graph for JEE




