
The circular boundary of the concave mirror subtends a cone of half angle
A)
B)
C)
D)
Answer
139.8k+ views
Hint: Multiple reflection of light is the reflection of light that happens between reflecting surfaces many a times. If a light that is reflected from a surface is made to incident on another surface, this process is called multiple reflection of light.
Complete step by step solution:
When two mirrors are placed in front of each other, then multiple images are formed. This is because the image formed by one mirror will act as an object to the second mirror. This pattern continues and further images of image are formed. If the mirrors are placed at some angle to each other then the reflections produced will be curved. The number of reflections can be increased by increasing the number of mirrors. These days multiple reflection of sound waves principle is used to make a stethoscope used by doctors to check heartbeat or pulse rate.
An incident ray will suffer many reflections if it is incident on only one part of the mirror. It reflects in a perpendicular direction and intersects the other side of the mirror. This is obtained if the angle of incidence is
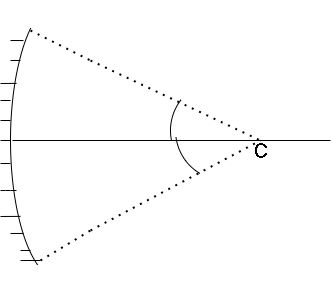
The minimum value for which the incident ray will suffer many reflections is
Option B is the correct answer.
Note: If the plane mirrors are used for multiple reflections and if the angle between the plane mirrors is
Complete step by step solution:
When two mirrors are placed in front of each other, then multiple images are formed. This is because the image formed by one mirror will act as an object to the second mirror. This pattern continues and further images of image are formed. If the mirrors are placed at some angle to each other then the reflections produced will be curved. The number of reflections can be increased by increasing the number of mirrors. These days multiple reflection of sound waves principle is used to make a stethoscope used by doctors to check heartbeat or pulse rate.
An incident ray will suffer many reflections if it is incident on only one part of the mirror. It reflects in a perpendicular direction and intersects the other side of the mirror. This is obtained if the angle of incidence is

The minimum value for which the incident ray will suffer many reflections is
Option B is the correct answer.
Note: If the plane mirrors are used for multiple reflections and if the angle between the plane mirrors is
Recently Updated Pages
Average fee range for JEE coaching in India- Complete Details

Difference Between Rows and Columns: JEE Main 2024

Difference Between Length and Height: JEE Main 2024

Difference Between Natural and Whole Numbers: JEE Main 2024

Algebraic Formula

Difference Between Constants and Variables: JEE Main 2024

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility, & More

JEE Main 2025: Derivation of Equation of Trajectory in Physics

A point charge + 20mu C is at a distance 6cm directly class 12 physics JEE_Main

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

Electric Field Due to Uniformly Charged Ring for JEE Main 2025 - Formula and Derivation

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Degree of Dissociation and Its Formula With Solved Example for JEE

Electric field due to uniformly charged sphere class 12 physics JEE_Main

Dual Nature of Radiation and Matter Class 12 Notes: CBSE Physics Chapter 11

Formula for number of images formed by two plane mirrors class 12 physics JEE_Main




