Question

The condition for obtaining secondary maxima in the diffraction pattern due to single slit is:
A) $a\sin \theta = \dfrac{{n\lambda }}{2}$
B) $a\sin \theta = \dfrac{{(2n - 1)\lambda }}{2}$
C) $a\sin \theta = n\lambda $
D) $a\sin \theta = (2n - 1)\lambda $

Answer 1

Hint: Diffraction of light is the property of light bending around the corners such that it spreads out and illuminates areas. Diffraction is really hard to distinguish from interference as both occur simultaneously.

Complete answer:
The diffraction from a single slit gives a characteristics pattern. Diffusion effects are usually noticeable with the slit with size not very much larger than the wavelength.

The above diagram represents a laser illuminating a single slit and a double slit and the resultant pattern is projected on the screen. The pattern is maximum at centre as the light travels from an equal distance from the slit .The central pattern is broad and is equally spaced from either side with weaker maxima.
For calculating first order minima, assuming a slit width a and divide it in two equal halves .From Huygens principle and considering parallel rays from the both sides at angle to the axis of symmetry.
The ray that will come from a distance of a/2 from below will travel extra distance $\left( {a\sin \dfrac{\theta }{2}} \right)$ when the distance is half the wavelength then $a\sin \theta = \lambda .$
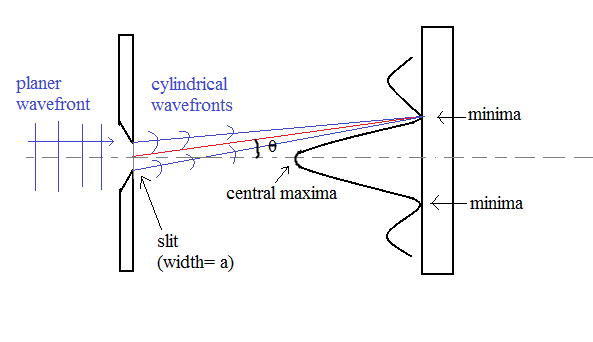For maxima, the distance between two nth second maxima with central maxima is calculated
as: ${x_n} = D\theta = \dfrac{{(2n + 1)}}{{2b}} = \dfrac{{(2n + 1)\lambda f}}{{2b}}$
Where \[b = a\] (width of the slit)
Therefore the diffraction pattern due to single slit for secondary maxima is:
$a\sin \theta = (2n - 1)\dfrac{\lambda }{2}$
Where, $n = 2,3,4,..$

Hence option (B) is the correct option.

Note: Diffractions are only observed with waves travelling in two dimension or three dimension. Diffraction is interference phenomenon where interference of an infinite number of waves emitted by a continuous distribution of source points in two or three dimensions.