Question

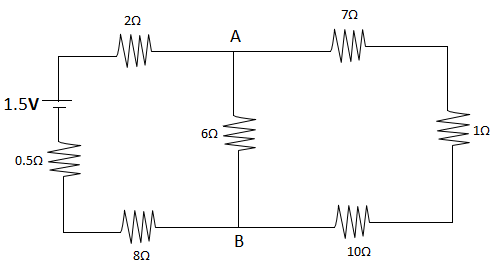
The current from the battery in the circuit diagram shown is:

A) $1A$
B) $2A$
C) $1.5A$
D) $3A$

Answer 1

Hint: We will apply here Kirchhoff’s second law, i.e., $\sum ir = \sum e$. It is an application of mesh analysis. After analyzing the loops one by one by, we have to solve the two equations to get the value of the current.

Formula used:
let, the current from the battery in the loop is $i$ and resistance of the loop is $r$. Then the product of these two will be the electromotive force acting in that loop, i.e., $\sum ir = \sum e$.

Complete step by step solution:
Kirchhoff formulated two laws. One is Kirchhoff’s first law or Kirchhoff’s current law (KCL). It states that in an electrical circuit (or network of wires) the algebraic sum of currents through the conductors meeting at a point is zero, i.e., $\sum i = 0$.
Another one is Kirchhoff’s second law or Kirchhoff’s voltage law (KVL). It states that the algebraic sum of the product of the current and resistance in any closed loop of a circuit is equal to the algebraic sum of electromotive force acting in that loop, i.e., $\sum ir = \sum e$
The given circuit is a mesh, a complicated circuit formed by a number of adjacent loops. So, it can be analyzed one by one by applying Kirchhoff’s second law.
Let, current ${i_1}$ flow in the 1st mesh and current ${i_2}$ flow in the 2nd mesh.
Now, applying Kirchhoff’s second law in the mesh 1, we get,
$2{i_1} + 6{i_1} - 6{i_2} + 8{i_1} + 0.5{i_1} = 15$
or, $16.5{i_1} - 6{i_2} = 15$ $ \ldots \left( 1 \right)$
Applying Kirchhoff’s second law in the mesh 2, we get,
$7{i_2} + {i_2} + 10{i_2} + 6{i_2} - 6{i_1} = 0$
or, $24{i_2} - 6{i_1} = 0$
or, $4{i_2} - {i_1} = 0$ $ \ldots \left( 2 \right)$
From equation $\left( 2 \right)$ we get, ${i_1} = 4{i_2}$
Putting the value of ${i_1}$ in the equation $\left( 1 \right)$, we get,
$16.5 \times 4{i_2} - 6{i_2} = 15$
or, $66{i_2} - 6{i_2} = 15$
or, $60{i_2} = 15$
or, ${i_2} = \dfrac{{15}}{{60}} = \dfrac{1}{4}$
Now, putting this value of ${i_2}$ in equation $\left( 2 \right)$, we get,
$(4 \times \dfrac{1}{4}) - {i_1} = 0$
or, ${i_1} = 1$

So, the current from the battery in the circuit is $1A$.

Note: While applying this law, we have to keep in mind the sign convention. In traversing a loop, the currents flowing in the clockwise direction are taken as positive while currents flowing in the anticlockwise direction are taken as negative. Also, while traversing the loop, the electromotive force of the source, which sends current in the clockwise direction, is taken as positive and the emf of the source, which sends current in the anticlockwise direction, is negative.