Question

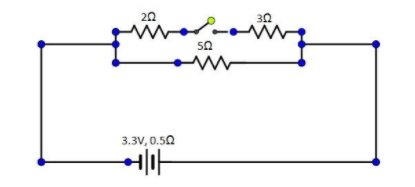
The diagram above shows a circuit with the key k open. Calculate

(A) The resistance of the circuit when the key k is open.
(B) The current drawn from the cell when the key k is open.
(C) The resistance of the circuit when the key k is closed.
(D) The current drawn from the cell when the key k is closed.

Answer 1

Hint: When the key k is closed, the current passes through the entire circuit and through all three resistors. When the key k is open, the current passes through the $5\Omega $ resistor only.
Formula Used: The formulae used in the solution are given here.
If the resistors are linked in series, the series resistance is articulated as- $R = {R_1} + {R_2} + {R_3} + ...$
If the resistors are linked in parallel, the series resistance is articulated as- $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ...$
By Ohm’s Law, we know that, $R = \dfrac{V}{I}$ where $R$ is the resistance, $V$ is the voltage across its ends and $I$ is the current.
$ \Rightarrow I = \dfrac{V}{R}$.

Complete Step by Step Solution: Resistance is the measure of opposition applied by any object to the flow of electric current. A resistor is an electronic constituent that is used in the circuit with the purpose of offering that specific amount of resistance.
If the resistors are linked in series, the series resistance is articulated as- $R = {R_1} + {R_2} + {R_3} + ...$
If the resistors are linked in parallel, the series resistance is articulated as- $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} + ...$
For the circuit given above, the resistors $2\Omega $ and $3\Omega $ are connected in series and both of them are connected to the $5\Omega $ resistor in parallel.
The entire setup is connected to a source of electromagnetic force (emf) $3.3V$and $0.5\Omega $ source resistance.
(i)The resistance of circuit when key K is open:
When the key is open, the only resistance left will be the $5\Omega $ resistance in series with $0.5\Omega $ source resistance, hence net resistance =$R = 5 + 0.5 = 5.5\Omega $
(ii) The current drawn from the cell when the key k is open.
When the key is open, net resistance =$5.5\Omega $.
By Ohm’s Law, we know that, $R = \dfrac{V}{I}$ where $R$ is the resistance, $V$ is the voltage across its ends and $I$ is the current.
$ \Rightarrow I = \dfrac{V}{R}$.
Since $R = 0.5\Omega $ and $V = 3.3V$,
(iii) The resistance of the circuit when the key k is closed.
When the key K is closed, the current passes through the entire circuit, the $5\Omega $ will be in parallel with series combination of $2\Omega $ and $3\Omega $
Thus the resistance $R = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}} = \dfrac{{5 \times 5}}{{5 + 5}} = 2.5\Omega $
${R_{total}} = 0.5 + 2.5 = 3\Omega $
$\therefore $ The resistance of the circuit when the key k is closed is $3\Omega $.
(iv) The current drawn from the cell when the key k is closed.
When the key is closed, net resistance= $3\Omega $
Current $I = \dfrac{V}{R}$.
$\therefore I = \dfrac{{3.3}}{3} = 1.1A$

Current drawn when key K is closed is $1.1A$.

Note: Resistance is a measure of the opposition to current flow in an electrical circuit. Resistance is measured in ohms, symbolized by the Greek letter omega. Ohms are named after Georg Simon Ohm (1784-1854), a German physicist who studied the relationship between voltage, current and resistance. He is credited for formulating Ohm's Law.